You might have noticed that when you stretch a rubber, it tries to come back to its initial condition. Did you ever think why is the rubber trying to do so? If you don’t know the cause of such activity of rubber, let me tell you that this is caused by a property of the rubber, called elasticity. Not only in rubber, such elastic property can be seen in all substances. Elasticity is the property of a substance by which an object tries to maintain its original shape or size by opposing any deformating cause. Now, what happens if we try to deform the substance forcefully? Initially it tries to overcome the external effect, but if the external force is very large it cannot withstand and loses its shape. The deformation of shape or size of an object is scientifically termed as strain and the internal force per unit area arises in the object to overcome the external effect is known as stress. Detailed explanation of stress and strain along with stress vs strain curve are provided in the main content below. Stress and strain are very important topics in engineering and physics.
Definition of Strain
Strain is defined as the change in dimension (Length or Volume ) per unit original dimension of an object due to application of external force. For example, if the length of a wire is changed by \small\delta L and its initial length is L, then the strain in the object is \small\frac{\delta L}{L}. Here, the dimension mentioned in the definition is the length of the object. Since, strain is the ratio of same physical quantities, it does not have any unit and dimensional formula.
Definition of Stress
When the shape or size of an object is changed or tried to changed, an internal force occurs inside the substance which tries to counter the external force. Stress is defined as the amount of internal force aries per unit area of the object to counter the strain in the object.
Equation for stress and strain
The equation of strain can be written as, \small Strain = \frac{Change \space in \space dimension}{Initial \space dimension}, [like \small\frac{\delta L}{L}].
The equation of stress is, \small Stress = \frac{Force}{Area} or, \small Stress = \frac{F}{A}.
Unit and dimensional formula of stress and strain
Strain is the ratio of same physical quantities. Therefore, strain is unitless and dimensionless.
Stress has the S.I. unit of N/m2 and C.G.S. unit of dyne/cm2. The dimensional formula of stress is equal to the dimension of force divided by dimension of area which becomes [ML-1T-2]. Thus, the unit and dimension of stress are same as the unit and dimension of pressure.
Stress vs Strain curve and Hooke's law of elasticity
The stress vs strain curve is shown in the following graph. It behaves like an elastic body in the region from point O to point B. After point B it becomes plastic body and breaks at point E.
- OA : Proportional limit
- CD : Strain hardening
- DE : Necking
- Point A : Elastic limit
- Point B : Upper yield point
- Point C : Lower yield point
- Point D : Ultimate Tensile Strength (UTS)
- Point E : Breaking point
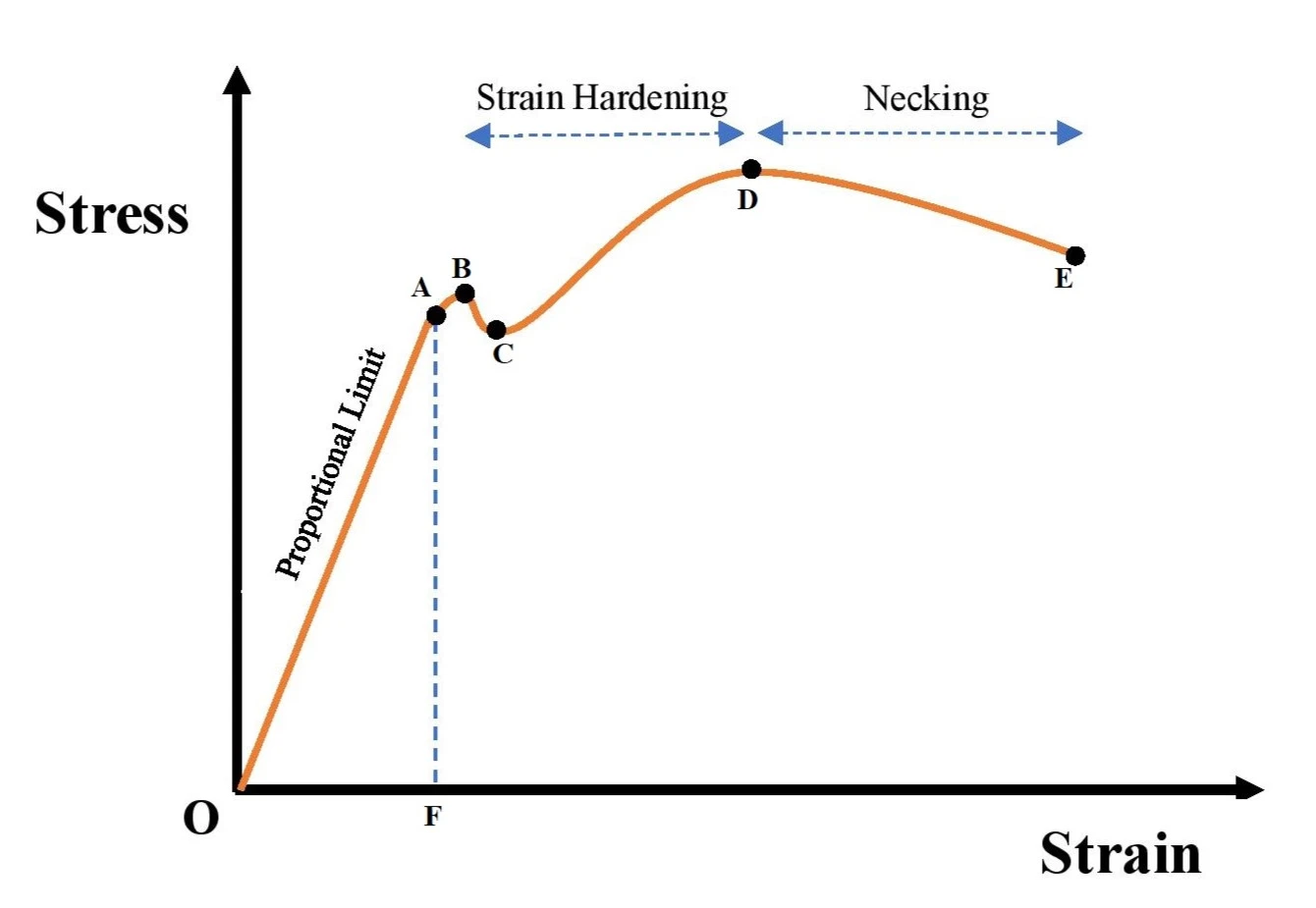
Explanation of Stress vs Strain graph
Stress vs Strain graph of a substance contains three regions -
- Proportional region
- Strain hardening region
- Necking region
Proportional Region:
In this region, stress in the substance is directly proportional to the strain. Proportional region is extended from point O to Point A in the given curve. The material can perfectly regain its origin shape and size in this limit once the external load is removed. Since it can completely overcome the deformation in this region, it is called elastic limit (more specificly, elastic limit is from point O to point B upto which the system is reversible). Hooke's law of elasticity is applicable for this region only. Hooke's law states that within the elastic limit, stress is directly proportional to the strain. The proportionality constant i.e. the ratio of stress to strain is nothing but the co-efficient of elasticity. The value of co-efficient of elasticity can be found from the proportional region of stress-starin graph which is equal to the slope of OA portion i.e. the ratio \small\frac{AF}{OF} in this case.
Yield point:
Point B and point C in the graph are the yield points. B is the upper yield point where the plastic behavior starts. Stress to strain ratio starts to decrease rapidly. Point C is the lower yield point where stress stops falling and take a very small pause.
Plastic limit:
Plastic limit extends from point B to point E i.e. from yield point to break point. This region includes strain hardening and necking. In this region, the deformation is not reversible i.e. the object cannot get its original shape and size back. Plastic limit includes the strain hardening and necking portion.
Strain hardening:
We saw that around the point C the object tries to overcome the strain again. This indicates that the substance becomes stronger after yielding. In the strain hardening region, the stress in the substance rises consistently with the increasing strain in it. At point D, the stress becomes maximum. This point is called ultimate tenstile strength (UTS).
Necking:
After point D, the strength of the material starts decreasing again. In this region, the thickness of the material decreases consistently ultill it breaks. This decrease in thickness or cross-section is termed as necking.
Different types of Stress and strain
There are mainly three types of stress and strain -
- Longitudinal stress and longitudinal strain
- Volume stress and volume strain
- Shearing stress and shearing strain
When the deformation occurs in the length of the object, the starin is called longitudinal strain which is the ratio of change in length to the initial length and the corresponding stress i.e. force per unit area is longitudinal stress. When the dimension is taken as volume, the strain is called volume strain. Thus the volume strain is the ratio of change in volume to the initial volume of the substance. Mathematically, \small volume \space strain = \frac{\delta V}{V}. The internal force arises in the object per unit area to overcome volume strain is the volume stress. In case of liquids or gases, volume stress is nothing but pressure. When a shreaing force is applied on an object to move a side or part of an object by an angle, the strain is known as shearing strain. A contact force is required in this case. Shearing stress has the same formula as force per unit area. All three types of stress and strain can be seen in solid substances, but longitudinal stress-strain and shearing stress-strain are not applicabe for liquids and gases.
Comparison between stress and strain
The differences between stress and strain are as follows -
| Serial No. | Stress | Strain |
| 1. | Stress is the measure of force per unit area. | Strain is the measure of deformation in the material. |
| 2. | Stress indicates how hard to deform an object. | Strain indicates how much deformation a force can do in an object. |
| 3. | Stress has units and dimension. | Strain does not have units and dimension. |
This is all from this article related to stress and strain, their equations, graph and differences. If you still have any doubt, you can ask me in the comment box. Also you can mention a topic on which you need a new article or explanation. Keep visiting this website.
Thanks.