Faraday’s law of Induction – Statement, formula

by

Scientist Oersted observed that a current carrying wire produces magnetic field around it. One can find the magnitude of the magnetic field by using Biot-Savart law and Ampere’s circuital law. The direction of the magnetic field can be found by using Fleming’s right hand Thumb rule and Maxwell’s corkscrew rule. Have you ever wondered if the reverse case is possible or not? That means, will a current flow through the wire if we place it in a magnetic field? Well, the curious Faraday has found it and gave two laws on this finding. In this article, I’m going to explain the Faraday’s law of electromagnetic induction and its equation.

Contents in this article:

  • What is electromagnetic induction?
  • Laws of Electromagnetic Induction
  • Faraday’s Law of electromagnetic induction
  • Lenz’s Law of Electromagnetic Induction
  • Equation of Faraday’s law
  • Law of conservation of energy from Lenz’s law

What is Electromagnetic Induction?

Electromagnetic induction is an electromagnetic process in which an EMF induces in a conducting coil when it is placed in a varying magnetic field. If there is a relative velocity between the magnetic field and coil, the magnetic flux linked with the coil changes. Due to this change in magnetic flux, an EMF induces in the coil.

Laws of Electromagnetic Induction

There are three laws of electromagnetic induction –

  • Faraday’s first law
  • Faraday’s second law
  • Lenz’s law

These laws give the causes of induction, equation or magnitude and the direction of the induced EMF and current.

Faraday’s law of Electromagnetic induction

Scientist Michael Faraday first observed that an EMF induces and thereby a current flows in a closed coil if there is any change in magnetic flux through the coil. Then he has given two laws on this. His first law gives the cause of induced EMF and the second law gives an equation to find magnitude of the induced EMF.

Faraday’s First law of Electromagnetic Induction

Faraday’s first law states that whenever the magnetic flux linked with a coil changes, an EMF induces in that coil and the induced EMF exists as long as the change in magnetic flux continues.

This law explains how an EMF induces in a coil in presence of variable magnetic field.

Explanation:

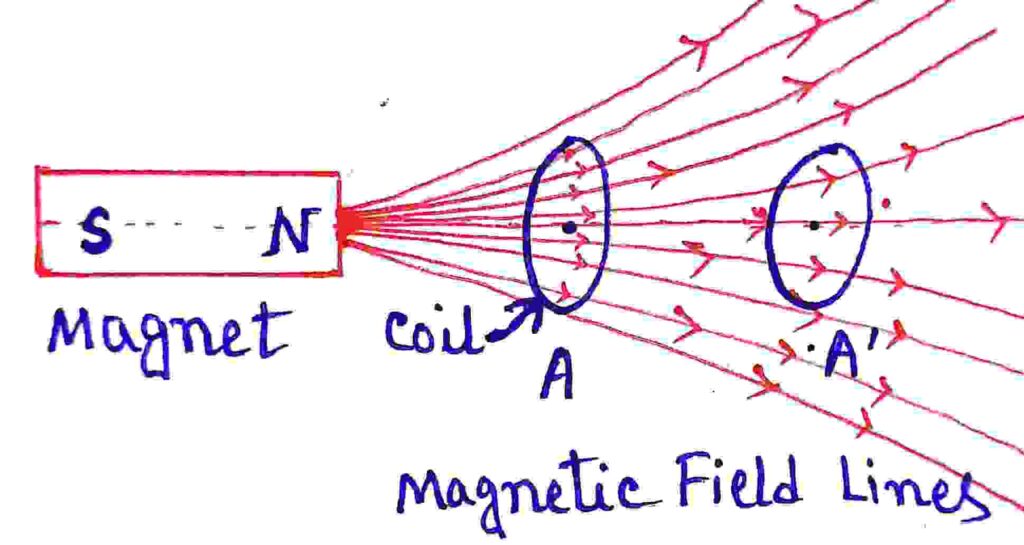
Faraday's First law of Electromagnetic Induction diagram
Induction of a coil

Number of magnetic field lines passing through the coil gives the amount of magnetic flux in the coil. In the diagram one can see that the number of magnetic field lines passing through the coil is 8 when it is at the position-A. Now when the coil is moved from position-A to position-A’, the number of field lines passing through it reduced to 3 . That means the magnetic flux through the coil changes due to the relative motion of the coil with respect to the magnetic field or magnet. Faraday said, this will induce an EMF in the coil. But if we stop the relative motion of coil, the induced EMF vanishes.

Faraday’s second law of Electromagnetic Induction

Faraday’s second law gives an equation to find the magnitude of Induced EMF. The second law states that the magnitude of induced EMF is directly proportional to the rate of change in magnetic flux linked with the coil.

If d\phi is the change in flux through the coil in the time interval dt, then according to Faraday’s second law, the magnitude of Induced EMF in the coil is \varepsilon \propto \frac{d\phi }{dt}.

Lenz’s Law of Electromagnetic Induction

Lenz’s law of electromagnetic induction gives the direction of induced EMF. This law states that the direction of induced EMF in the coil will be such that it will oppose the cause of its generation in the coil. That means induced EMF will oppose the change in flux through the coil or it opposes the relative motion between the coil and the magnet. So, induced EMF and change in magnetic flux in the coil are opposite effect to each other.

Equation for Faraday’s and Lenz’s law

From second law of Faraday we get the magnitude of induced EMF and from Lenz’s law we get the direction of induced EMF. Combining both laws we have the equation for induced EMF in a coil due to electromagnetic induction as, \varepsilon = - N \frac{d\phi }{dt}. Where, N is the number of turns in the coil. The negative sign arises from Lenz’s law which states that induced EMF will oppose the change in magnetic flux. Induced EMF has the unit of Volt.

If R be the resistance of the closed coil, then induced current through the coil will be i(t) = -N\frac{1}{R}\frac{d\phi }{dt}. Induced current has the unit of Ampere. Induced EMF and induced current both are the function of time.

Law of conservation of energy from Lenz’s law

Lenz’s law obeys the law of conservation of energy. One can obtain the explanation of law of conservation of energy from Lenz’s law.

Lenz’s law states that induced EMF or the current opposes its cause i.e. change in magnetic flux which occurs due to the relative motion between the coil and the magnet. Thus, the induced current opposes the relative motion of the coil. So, to move the coil an external mechanical work is to be done. Again, this movement will induce current in the coil. So, the external mechanical energy is converting into the electrical energy (current) in the coil. This is nothing but the law of conservation of energy.

Summary

Let’s have a quick summary of what we learned here!

  1. Faraday’s first law tells the causes of electromagnetic induction.
  2. Faraday’s 2nd law gives the measurement of induced EMF.
  3. Lenz’s law helps to find the direction of induced EMF.
  4. Lenz’s law obeys the law of conservation of energy.

This is all from this article on Faraday’s law of induced EMF. If you have any doubt on this topic you can ask me in the comment section.

Thank you!

Related Posts:

  1. Induced Voltage across an Inductor in AC circuit
  2. Working formula of Transformer
  3. Origin and Definition of Magnetic field
  4. Electromagnetic waves