Formula for Center of Mass by integration in Physics

by

All bodies consist of a large number of point masses. The mass of an entire body is the sum of the masses of those points. Now, there must be a central point in a body. If the body is symmetric and has a uniform density, then the central point is the center of mass of the body. In this article, I’m going to explain the center of mass, will derive its formula by integration and will discuss why it is important in Physics.

Contents in this article:

  1. Definition of center of mass
  2. Formula for center of mass
  3. Units of center of mass
  4. Examples of center of mass
  5. How to find center of mass by integration?

Definition of Center of Mass in Physics

The center of mass of a body is a point where its entire mass is considered to be concentrated. For a symmetric body with uniform density, the center of mass is its geometrical center i.e. its centroid or midpoint. But, for a body with non-uniform density, the center of mass shifts towards the portion of greater density.

Formula for Center of Mass

Since the center of mass shifts towards the denser side for a non-uniform body, a formula is needed to find its exact position. There can be different equations depending on the type of distribution of mass in the system. We are going to introduce those equations one by one.

Center of mass equation for a discrete mass system

Let a discrete system where the masses m1, m2, m3,……,mn are located at r1, r2, r3,….,rn respectively. Then the equation of center of mass of the discrete system is, \color{Blue}r_{c}=\frac{m_{1}r_{1} + m_{2}r_{2} + m_{3}r_{3} +....}{m_{1}+m_{2} + m_{3} +...}

or, \color{Blue}r_{c}=\frac{1}{M}(m_{1}r_{1} + m_{2}r_{2} + m_{3}r_{3} + ....) ……..(1)

Here, M is the mass of the entire system which is the sum of the masses in that system.

If the mass is distributed along X-axis then x1, x2, x3,…. should be written in place of r1, r2, r3,… of equation-(1). Similarly, this is true for other axes.

Formula for Center of Mass by integration for a continuous body

To find the center of mass of a continuous body, we need to use an integral equation. Let, M be the mass of the body and dm is the mass of an elementary part of the body at r distance from the origin.

Then the formula for center of mass of the continuous body is, \color{Blue}r_{cm}=\frac{\int r.dm}{\int dm}……..(2)

When the body is extended along X-axis, \color{Blue}x_{cm}=\frac{\int x.dm}{\int dm}.

Similarly, \color{Blue}y_{cm}=\frac{\int y.dm}{\int dm}

and, \color{Blue}z_{cm}=\frac{\int z.dm}{\int dm}

Then the position of center of mass is, (xcm, ycm, zcm)

Equation-(2) is the integral equation of center of mass for a continuous body.

Units for Center of Mass

The center of mass is actually the position (or distance from the origin) of the net mass of the body. So, its units and dimension are the same as those of distance.

SI unit of center of mass is meter (m) and CGS unit is centimeter (cm).

Examples of Center of Mass

  1. The center of mass of uniformly symmetric bodies like a sphere, ring, cylinder, etc. is their center point.
  2. We cannot say the center of mass for a non-uniform body. We need to calculate it using the above equations. One example is shown below.

Note: Uniform ring is an example for which the center of mass is outside the body. It is at its center which is not inside the material.

How to find Center of Mass by integration?

To calculate the position of the center of mass from the integral equation, you need to follow the following steps.

We need to find xcm, ycm and zcm. First, we are going to know the way to find xcm.

  1. Find the mass dm of the body for an elementary length dx at x distance from the origin. If the variation of mass is given as a function of distance, say m(x), then the mass of elementary length dx is, dm = m(x).dx
  2. Then find the xcm using the above equation of xcm.
  3. Similarly, find ycm and zcm after finding dm for dy and dz length respectively.
  4. Don’t forget to use the limits of the integration.
  5. Then the center of mass of the body is (xcm, ycm, zcm).

The linear density of a thin rod of length 1 meter along x-axis is \color{Blue}\lambda=2x. Find the center of mass of the rod.

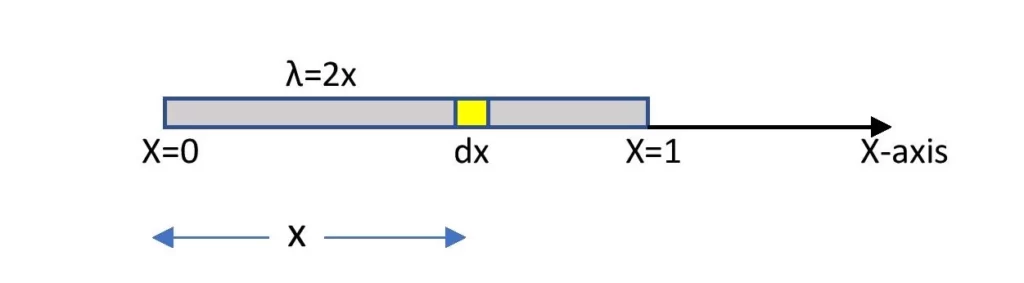
The linear density, \lambda=2x. Let, one of the ends of the rod is at the origin. Then another end is at x=1 m. So, the rod is extended from x=0 to x=1 m.

We choose an elementary length dx of the rod at a distance x from the origin (one end of the rod). Then the mass of that dx length is,

dm=\lambda.dx

or, dm=2x.dx.

Then the position of center mass along X-axis is, \color{Blue}x_{cm}=\frac{\int x.dm}{\int dm}

or, \color{Blue}x_{cm}=\frac{\int_{0}^{1} x.2x.dx}{\int_{0}^{1} 2x.dx}

or, \color{Blue}x_{cm}=\frac{\int_{0}^{1} 2x^{2}.dx}{\int_{0}^{1} 2x.dx}

Thus, \color{Blue}x_{cm}=\frac{2}{3} m

Now, the rod is thin along the y and z directions. So, the \color{Blue}y_{cm}=0 and \color{Blue}z_{cm}=0.

So, the position of center of mass of the rod is at (\color{Blue}\frac{2}{3}, 0, 0) m from one of the ends of the rod. In this way, one can find the center of mass of a continuous body by using the formula for center of mass by integration.

This is all from this article on the Center of mass and the integral formula of center of mass. If you have any doubt on this topic you can ask me in the comment section.

Thank you!

Related posts:

  1. Velocity center of mass
  2. Acceleration center of mass

1 thought on “Formula for Center of Mass by integration in Physics”

  1. Pingback: Velocity of center of mass - equation, calculation | Edumir-Physics

Comments are closed.