Formula for Surface charge density of sphere, cylinder and capacitor

Electric charges can be distributed along the length, over the surface and in the volume of a conductor. The density of electric charge refers to the amount of charges per unit dimension. There are three types of charge densities for the three types of distributions of charge. The Linear charge density and Volume charge density have been discussed in other two articles. In this article, we’re going to discuss the definition, unit and formula of Surface charge density of different conductors like a sphere, a cylinder and a capacitor.

Contents of this article:

What is Surface charge density

Formula of surface charge density
Units
Dimension

Surface charge density of different shaped conductors
Dependence on the curvature of the surface

What is Surface charge density of conductors?

Surface charge density of a conductor is defined as the amount of charge distributed per unit surface area of the conductor. It is denoted by the Greek letter sigma ( ${\color{Blue} \sigma }$ ). One cannot obtain surface charge density in a very thin linear conductor. Apart from that, surface charge distribution exists on every charged conductor.

The general formula of surface charge density

If Q amount of electric charge is distributed over the surface of a conductor of total surface area A, then

The general formula of surface charge density of the conductor is $\small {\color{Blue} \sigma =\frac{Q}{A}}$ …….(1)

Different conductors of the same amount of charge can have different surface charge densities. Because it depends on the area and curvature of the surface.

Units of Surface Charge density

Unit of Surface charge density = Unit of charge/unit of area

The SI unit of charge is Coulomb (C) and the SI unit of surface area is m². Therefore,

The SI unit of surface charge density is C/m² and its CGS unit is esu/cm².

Dimension of surface density of charge

The dimension of electric charge is [TI] and the dimension of surface area is [L²].

Hence the dimensional formula of Surface charge density of a conductor is [ L^-2TI ].

Formula for surface charge density of different conductors

The conductors of different shapes have different surface areas and hence they have different equations of surface charge density. Here we’re going to explore the surface charge density formula for a sphere or spherical shell, a cylinder, and a capacitor.

Formula of surface charge density of a sphere

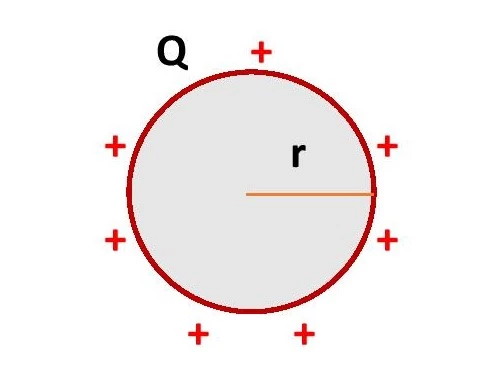
Consider a conducting sphere of radius r containing the total charge Q on its surface. The surface area of the sphere is A = 4πr². Using equation-(1) we get,

The formula for surface charge density of a conducting sphere is $\small {\color{Blue} \sigma =\frac{Q}{4\pi r^{2}}}$ …….(2)

The charge density on the surface of a conducting spherical shell is also the same as that of a conducting sphere of the same radius and the same charge. Since the curvature of the surface of a sphere is the same at every point on its surface, the surface charge density is constant everywhere on the surface of a sphere.

Formula of surface charge density of a Cylinder

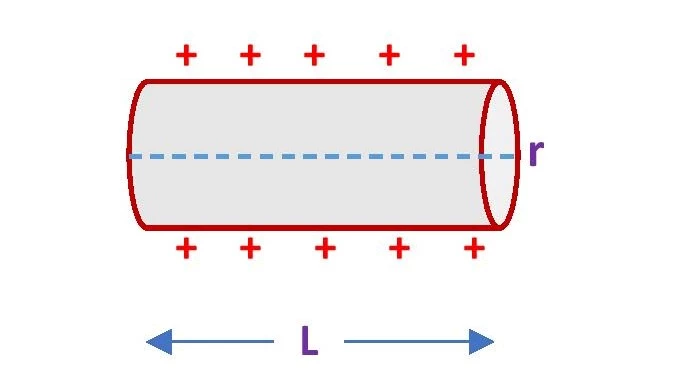
Consider a cylindrical conductor of length L, radius r. A cylinder has three surfaces – one curved surface and two flat surfaces. The density of electric charge is different for these two types of surfaces. The area of the curved surface is 2πrL and that of each of the flat surfaces is πr². Then,

The formula of charge density on the curved surface of the cylinder is $\small {\color{Blue} \sigma = \frac{Q}{2\pi rL}}$

and the charge density on flat surfaces of the cylinder is $\small {\color{Blue} \sigma = \frac{Q}{\pi r^2}}$ .

Where Q is the charge on the surface. The above two equations give the formula for the surface charge density of a cylinder.

Formula for surface charge density of a Capacitor

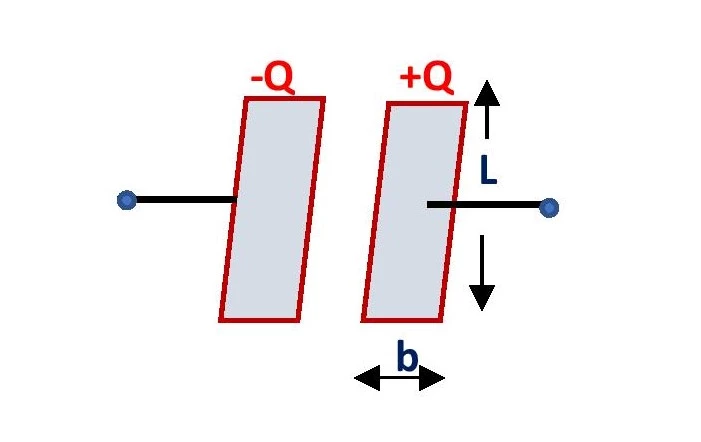
The formula for surface charge density of a capacitor depends on the shape or area of the plates. If the capacitor consists of rectangular plates of length L and breadth b, then its surface area is A = Lb. Then,

The surface charge density of each plate of the capacitor is $\small {\color{Blue} \sigma = \frac{Q}{Lb}}$

If the plates of the capacitor have the circular shape of radius r, then the equation of surface charge density of the capacitor will be $\small {\color{Blue} \sigma =\frac{Q}{\pi r^{2}}}$ .

Surface charge density of a conductor of irregular shape

For a conductor of an irregular surface, the surface area is different at different segments of its surface. The charge density depends on the curvature of the surface. The value of surface charge density will be greater at that region where the curvature is greater.

That means the surface charge density is greater at its edges. There is no permanent formula of surface charge density for an irregular-shaped conductor.

How does the surface charge density vary with the curvature of the surface?

Surface charge density depends on the curvature of the conductor. It has a greater value if there is a greater curvature. That means at the edges, the surface charge density is greater. This can be understood by using an example.

For a spherical conductor, the expression for surface charge density is $\small {\color{Blue} \sigma =\frac{Q}{4\pi r^{2}}}$ . Now, greater curvature means a lower radius. The denominator of this equation becomes smaller for a greater curvature (smaller radius). Therefore, the surface charge density increases with the increase in curvature of the surface of the conductor.

How to calculate surface charge density?

If you talk about finding the value of any physical quantity then you need to use the formula for that. In the above, we already have disclosed some equations of surface charge density. To find the surface density of charge we just need to know the values of the total electric charge on the surface of the conductor and the total surface area of the conductor. Then we need to use any suitable equation of surface density of charge from above to find it.

Let’s understand this by solving a numerical problem.

Surface charge measurement

The surface charge density of a spherical conductor of radius 10 cm is 0.7 C/m². Find the total charge on its surface.

Surface charge density, ${ \sigma }$ = 0.7 C/m²

Radius of the sphere, r = 10 cm = 0.1 m

Then, the surface area of the sphere is A = 4πr² = {4×3.14×(0.1)²}

or, A = 0.1256 m²

Thus, the total charge on the surface of the sphere is, Q = ${ \sigma }$ A

or, Q = (0.7×0.1256) = 0.8792

or, Q = 0.88 Coulomb (Up to two significant figures)

This is all from this article on the formula for surface charge density of different conductors. If you have any doubts about this topic, you can ask me in the comment section. If you need to find an expert to get physics homework help online you can visit professional physics assignment helpers.

Thank you!

Related Posts:

Charge density formula