Electric potential energy formula

In other articles, we became to know that an electric charge can produce an electric field around it and one can use Gauss’s law to find the electric fields due to charged conductors. This electric field is responsible for the electrostatic force between the charges. As a result, charged particles move in the electric field region. Since the movement of a particle (whether it is charged or not) due to external force gives the work done on the particle, the electrostatic force works on the charged particles. This work done by the electric force on an electric charge is stored as the potential energy of the charge. In this article, we are going to discuss the definition, formula, units of electric potential energy.

Contents in this article:

1. Electrostatic potential energy
2. Formula of electrostatic potential energy
3. Units of electric potential energy
4. Expression for the minimum velocity of a charge to cross a potential difference

What is electrostatic potential energy?

To move a positive charge from a lower potential to a higher potential region, an external agent needs to work. This work done is stored as the potential energy in the electric field. This is called the electrostatic potential energy. So, the work done to move a positive charge against an electric field is the electric potential energy of the electric charge.

Electric potential energy formula

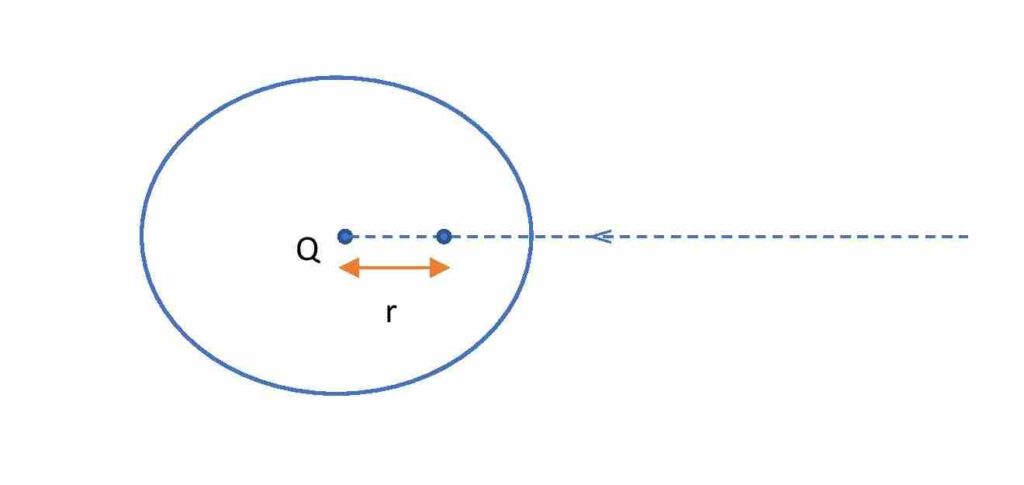
The work done by the external agent to move a charge through a potential difference is stored as the electrostatic potential energy in the electric field.

Now, electric potential V is the work done per unit charge. So, the work done in moving a charge q through a potential difference V is equal to qV.

Thus, the formula for electrostatic potential energy, W = qV………..(1)

Now, If V_A and V_B be the electric potentials at points A and B respectively, then the potential difference between these points is V_AB = (V_A-V_B). Then electrostatic energy required to move q charge from point-A to point-B is,

W = qV_AB

or, W = q(V_A-V_B) ……………(2)

Again, the formula for electric potential at r distance from a point charge Q is \color{Blue}V=\small \frac{Q}{4\pi \epsilon _{0}r}.

Then from equation- (1), the electrostatic potential energy to bring a charge q from infinity to r distance of a source charge Q is,

\small {\color{Blue}W= \frac{qQ}{4\pi \epsilon_{0}r}} ………….(3)

This is the electrostatic potential energy formula.

Units of electrostatic potential energy

The units of electric potential energy are similar to that of the energy we know. So, its SI unit is Joule (J) and the CGS unit erg.

Dimensional formula of electric potential energy

The dimensional formula for electric potential energy is the same as that of the normal energy we know. Thus, it has the dimension of [ML²T^-2].

Expression for minimum velocity of a charge q to cross a potential difference V

Let an electric charge q is to cross a potential difference V with a velocity u. Now, the kinetic energy of the charge will be used to do the electrostatic work to overcome the potential difference. This satisfies the law of conservation of energy.

So, \color{Blue}\frac{1}{2}mu^2= qV

or, \color{Blue}u=\sqrt{\frac{2qV}{m}} …………..(9)

This is the minimum velocity that a charged particle requires to cross the potential difference. For an electron, we need to replace q by the charge of an electron e.

Homework problems on electric potential energy

1. Find the electric potential at 10 cm from a point charge 80 micro-Coulomb. If we place another charge of 2 micro-coulomb at that point, then what will be the electrostatic potential energy of the system of these two charges?
2. Find the minimum velocity that an electron should have to cross a potential difference of 20 volts.

Summary

In this article, we became to know what is electric potential energy and its formula, units and dimension. Also, we have derived the electric potential energy formula by using equation for electrostatic potential for a point charge.

This is all from this article on the definition, units and formula of electrostatic potential energy. If you have any doubt on this topic you can ask me in the comment section.

Thank you!

Related posts:

1. Electrostatic Potential
2. Equipotential surface and its properties
3. Gauss’s law in electrostatics
4. Potential energy stored in a Capacitor