Properties of Equipotential surface in uniform electric field

We have learned the electric Potential and potential energy in other articles. In this article, we are going to discuss the equipotential surface and its properties. Here we will consider that the equipotential surface in a uniform electric field. That means the strength of the electric field is equal at every point and electric field lines are straight and parallel lines.

What is an equipotential surface?

A surface will be called an equipotential surface if the electrostatic potential at every point on the surface is equal. All real or imaginary surfaces satisfying this property are equipotential surfaces.

Examples of Equipotential surfaces

Here are some examples of equipotential surfaces –

The surface of a charged sphere is an equipotential surface.
Any imaginary spherical surface around a point charge is an equipotential surface.
All the circular plane surfaces perpendicular to an electric dipole and at the middle of the dipole are equipotential surfaces.

Properties of Equipotential surface

Basic properties of an equipotential surface are as followings –

The electric potential at every point on an equipotential surface is equal.
No work is to be done to move an electric charge from one point to another point on an equipotential surface. Because the potential difference between the points is zero.

Electric field lines intersect equipotential surfaces perpendicularly. That means a uniform electric field is also perpendicular to the equipotential surface.
Any two equipotential surfaces cannot intersect each other.
Surfaces of all the charged conductors are equipotential surfaces.

Equipotential surfaces for a Point Charge

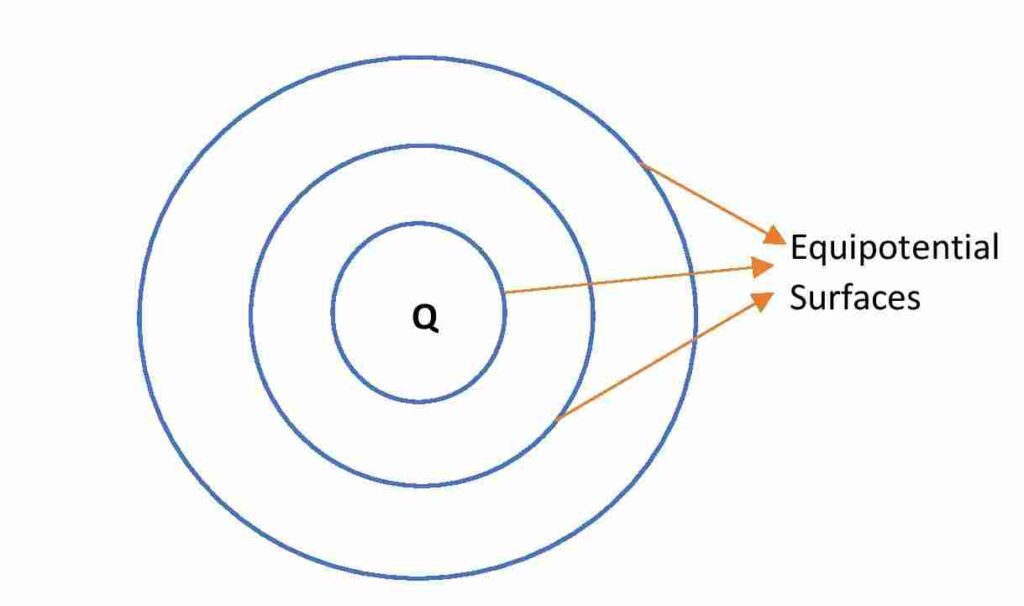
All equipotential surfaces around a point charge are the spherical surfaces of different radii. For each surface the potential is different , but every points on a particular spherical surface have equal potential.

Equipotential surfaces for uniform electric field

All equipotential surfaces in a uniform electric field are square or rectangular shaped surfaces that are perpendicular to the electric field lines or the direction of electric field.

Equipotential surface of an electric dipole

For an electric dipole, the equipotential surfaces are the circular planes at the center of dipole that are perpendicular to the dipole. Imagine a circular disc perpendicular to the dipole in the middle of the dipole. Now, the circular plane in the middle of the dipole has zero electric potential at every point on it. So, this circular plane is an equipotential surface.

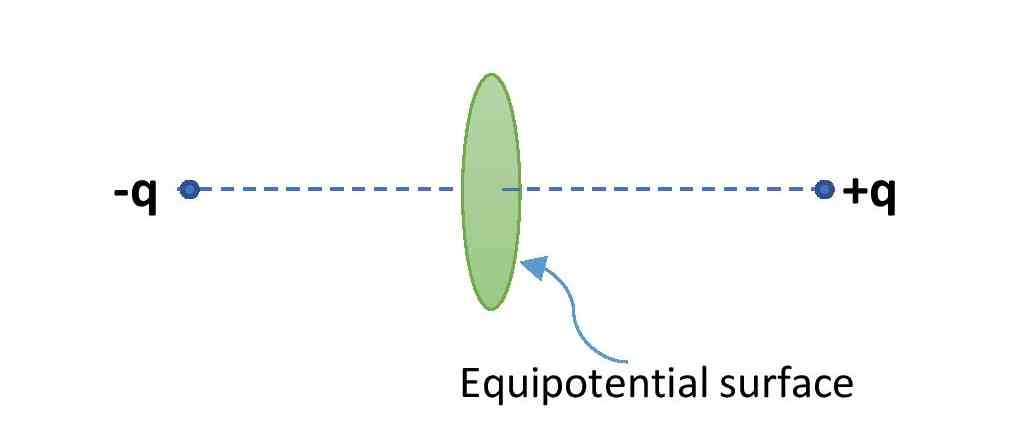
One can imagine an infinite number of co-centric circular planes or discs in the middle of the dipole. All these plane surfaces are equipotential surfaces.

Proof that electric field lines intersect equipotential surfaces perpendicularly

The tangent at any point on the electric field line gives the direction of the electric field at that point. So, in the uniform electric field, the direction of the field line is the direction of the electric field.

Now, let the electric field (E) intersects or crosses an equipotential surface with an angle $\small \theta$ . Then the tangential component of electric field i.e. the component of the electric field along the surface is Ecos $\small \theta$ .

**Diagram to prove that equipotential surfaces are perpendicular to electric field**

Now, we want to move a charge by a small distance r on the equipotential surface. The work done in moving the charge on the equipotential surface is zero.

So, work done, $\small W=Ecos \theta .r = 0$

Now, E and r are non-zero terms. Then, $\small Cos\theta =0$

or, $\small \theta$ = 90 degree

Thus, the electric field is perpendicular to the equipotential surface. Therefore, electric field lines cross the equipotential surface perpendicularly.

Summary

An equipotential surface is a real or imaginary surface having equal electric potential at every point on it. Electric field lines intersect equipotential surfaces perpendicularly in a uniform electric field. That means equipotential surfaces are perpendicular to the uniform electric field. There is no potential difference between any two points on the equipotential surface. So, no work is to be done to move a charge from one point to another point on the equipotential surface. The surface of a charged conductor is an equipotential surface.

This is all from this article. If you have any doubt on this topic you can ask me in the comment section.

Thank you!

Related Posts: