Coulomb’s law of electrostatics – equation, vector form

by

Electrostatics Article – 4:

In the previous article, we became to know that an electric charge can produce an electric field around it inside which it interacts with other charges. This interaction is nothing but the exertion of forces on the charges. This force between the electric charges is known as the Electrostatic Force. Coulomb’s law of electrostatics gives an equation for the electrostatic force between the charges. In this article, we are going to discuss Coulomb’s Law of electrostatics and its formula in vector form.

Contents of this article:

  • Fundamental Law of electrostatics
  • Coulomb’s law of electrostatics
  • Formula for Coulomb Law
  • Vector form of Coulomb Law
  • Derive Coulomb Law from Gauss’s Law
  • Application of Coulomb Law
  • Limitations of Coulomb’s law

Fundamental Law of electrostatics

We already know that electric charges exert forces on each other. The Fundamental law of electrostatics states that the electric charges of the same sign repel each other and the electric charges of the opposite signs attract each other. That means two positive charges or two negative charges repel each other. But if we place a positive charge near a negative charge, then they will attract each other.

Statement of Coulomb’s law in electrostatics

Coulomb’s law of electrostatics gives an expression for the electric force between the electric charges. This law states that the electrostatic force between two point charges separated by a distance is directly proportional to the multiplication between the magnitude of the charges and inversely proportional to the square of the distance between the charges.

Suggested Article: Electrostatic Force between electric charges.

Formula for Coulomb’s Law of electrostatics

+Q and +q charges are at r distance

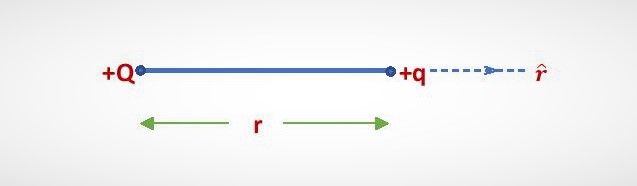
Let two point charges +Q and +q are placed at a distance of separation r. Then according to Coulomb’s law, the electric force (F) acting between the charges is,

\small {\color{Blue} F\propto Qq} and, \small {\color{Blue}F\propto \frac{1}{r^{2}}}

Then we get, \small {\color{Blue} F\propto \frac{Qq}{r^{2}}}

or, {\color{Blue}F=\frac{kQq}{r^{2}}} ………………….. (1)

Where k is Coulomb’s constant. It varies medium to medium.

In CGS unit, the value of k is 1 and in SI unit, k has an expression as {\color{Blue} k=\frac{1}{4\pi \epsilon _{0}}} in air medium or free space which have the value of 9×109. Here, \small {\color{Blue} \epsilon _{0}} is the permittivity of free space.

So, the equation for Coulomb’s law in air medium is, \small {\color{Blue} F=\frac{1}{4\pi \epsilon _{0}}\frac{Qq}{r^{2}}} …………… (2) in SI unit.

and, \small {\color{Blue} F=\frac{Qq}{r^{2}}} ………………. (3) in CGS unit.

For the other medium, one should use the permittivity of that medium in place of the permittivity of free space.

Vector form of Coulomb’s Law equation

In SI system, the magnitude of the electrostatic force is given by the equation-(2). Now, the force is repulsive for two positive charges +Q and +q. So, the force on q will act along the outward direction from q. We denote the unit vector by {\color{Blue} \widehat{r}} along the outward direction from q.

Then the vector form of Coulomb’s law is, \small {\color{Blue} \overrightarrow{F}=\frac{1}{4\pi \epsilon _{0}}\frac{Qq}{r^{2}}\widehat{r}} …….. (4)

Again, the position vector is, \small {\color{Blue} \overrightarrow{r}=r\widehat{r}}. Then, \small {\color{Blue} \widehat{r}=\frac{\overrightarrow{r}}{r}}……….. (5)

Now, from equation-(4) and equation-(5) one can get, \small {\color{Blue} \overrightarrow{F}=\frac{1}{4\pi \epsilon _{0}}\frac{Qq}{r^{3}}\overrightarrow{r}} ……… (6).

Equation-(6) is another form of the vector form of Coulomb’s law.

Derivation of Coulomb’s Law from Gauss’s Law

The equation of Coulomb law can be derived from the Gauss law of electrostatics.

According to the Gauss’s law of electrostatics, the electric flux passing through a spherical surface of charge Q and radius r is, \small {\color{Blue} \int \overrightarrow{E}.\overrightarrow{dS}=\frac{Q}{\epsilon _{0}}}.

Then the electric field on the surface of the sphere due the Q charge is, \small {\color{Blue} E=\frac{Q}{4\pi \epsilon _{0}r^{2}}}.

If we place another charge q on the surface of the sphere, the electrostatic force on the charge q will be, F = qE.

Now, putting the equation of E in F = qE we get, \small {\color{Blue} F=\frac{Qq}{4\pi \epsilon _{0}r^{2}}}.

This is nothing but Coulomb’s force equation. Hence, Coulomb’s Law is derived from Gauss’s law.

Application of Coulomb law

The only application of Coulomb’s equation is to find the electric force between the static electric charges. One can find the value of the electric field at any point by observing the Coulomb’s force at that point.

Limitations of Coulomb’s law

Here are some limitations of Coulomb law –

  1. Coulomb’s law is applicable only for the point charges. To apply this law for a large body its total charge is assumed to be located at a single point (at the Centre of charge) so that it can be treated as a point charge.
  2. This law is valid for the charges at rest with respect to the observer.
  3. Coulomb’s law is valid when the distance between the charges is greater than the nuclear distance or nuclear diameter (10-15m).

This is all from this article on Coulomb’s law of electrostatics and its formula in vector form. If you have any doubts on this topic you can ask me in the comment section. Do you know that the strength of the electrostatic force is directly related to the electric field lines or the electric lines of force? Click on the Next Article button below to read an article on electric field lines.

Thank you!

Related Posts:

  1. Electrostatic Force
  2. Electric charge
  3. Electric field
  4. Gauss’s law of electrostatics
Previous Article
Next Article