Newton’s laws of motion tell that translational motion is caused by a force. That means if we apply sufficient force on a body, it will move. But how to rotate an object? Can a force produce the rotational motion of a body? The answer will be yes, but not any type of force. For the rotation of an object, we need to apply a force or a pair of forces on the object in a certain way. In this context, the concepts of Torque and Moment of force are introduced. In this article, I’m going to explain how to rotate an object by applying a Torque.
Contents of this article:
- Definition of Torque in physics
- Equations for torque
- Rotation of an object about a fixed axis
- Direction of rotation
- Analogy between Translational and Rotational motion
Definition of Torque in Physics
When two equal and opposite forces act parallelly on an object, the multiplication between the magnitude of force and the distance between the lines of acting of forces produces a new physical quantity which is known as the Torque.
You might be wondering that two equal and opposite forces cancel each other, then how does a new physical quantity arise with this? Let me explain!
Two equal and opposite forces cancel each other when they act on the same point. Here the forces are acting parallelly at two different points, usually, one acts on the left side and another on the right side of a body. Therefore, these forces will not cancel but produce a Torque in the body.
Equations for torque
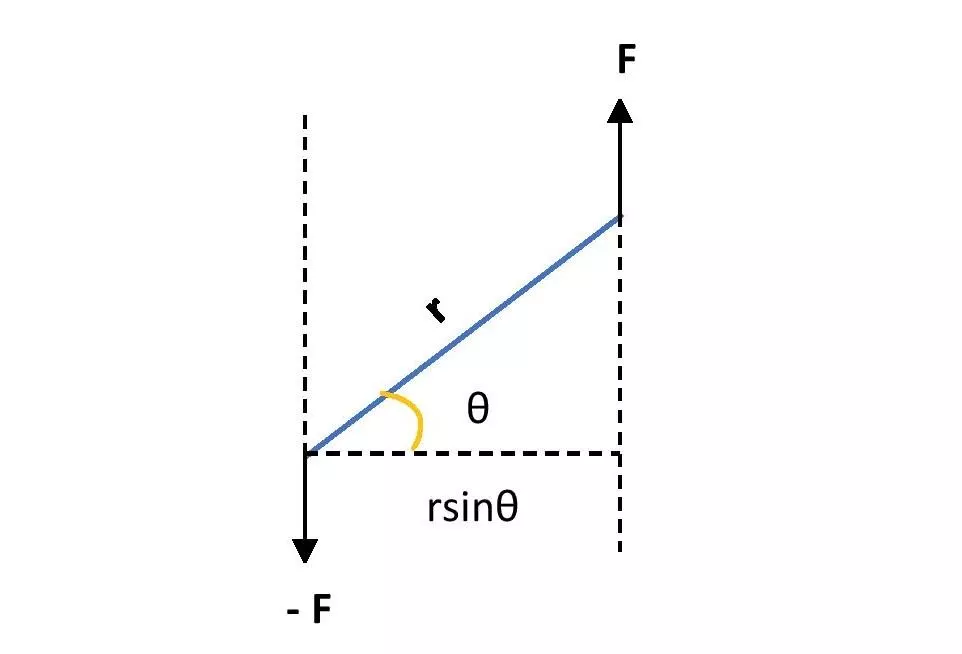
Let two forces F and – F act on a rod of length r. If the angle between the length of the rod and the applied force is \small\color{Blue}\theta, then the distance between the lines of acting of the forces is \small\color{Blue} r.sin\theta.
Then the equation of Torque on the rod is, \small \color{Blue}\tau = F.r.sin\theta.
Rotation of an object about a fixed axis
What causes the rotation of an object? A torque (two opposite and parallel forces) causes the rotation of a body about an axis. If the lines of acting of forces are not changed then the axis of rotation of the object will remain fixed.
A single force can rotate an object whose one of the ends is attached somewhere. A door is an example of such a body. For the rotation with a single force, the moment of force is the equivalent of the Torque.
Learn more about the Torque and Moment of force and how they are different from each other.
Direction of rotation of an object
There are two possible directions for a rotating body –
- Clockwise rotation
- Anti-clockwise rotation
Whether a body will rotate clockwise or anti-clockwise, depends on the direction of applied forces or torque. If the direction of the Torque is vertically upwards, then the direction of rotation will be anti-clockwise and vice-versa. The direction of rotation of a body can be determined by using Fleming’s Thumb rule.
Examples of rotating body in our daily life

There are plenty of examples of rotating body. Here are some of these –
- The motion of a ceiling fan.
- The motion of a Top.
- Motion of wheels of moving vehicles.
- Rotation of a rigid body.
Analogy between Translational and Rotational motion
Though Translation and Rotation are two different types of motion, we can relate the corresponding physical quantities and equations. That means if you know the equations of linear motion, then you can easily guess the rotational counterpart of those equations.
Sounds good? Let’s go for it! It is better to show these in tabular form.
Equivalent physical quantities in translation and rotation of an object
| SL. No. | Physical quantity in translational motion | Equivalent physical quantity in Rotational motion |
| 1 | Mass (m) | Moment of Inertia (I) |
| 2 | Displacement (x) | Angular displacement (\theta) |
| 3 | Velocity (v) | Angular velocity (\omega) |
| 4 | Acceleration (a) | Angular acceleration (\alpha) |
| 5 | Force (F) | Torque (\tau) |
| 6 | Linear Momentum (P) | Angular Momentum (L) |
Equations in translational and rotational motion
Again, we can write the equations of rotational motion from the equations of translational motion. Just need to replace the physical quantities with their rotational counterparts. For example, mass is to be replaced by Moment of Inertia, Force by Torque, etc. Go through the following table for this.
| Equation for | In translational motion | In rotational motion |
| Force (Newton’s 2nd law) | F=ma | \tau=I\alpha |
| 1st equation of motion | v=u+at | \omega_{2}=\omega_{1}+\alpha t |
| 2nd equation of motion | x=ut+\frac{1}{2}at^2 | \theta=\omega_{1}t+\frac{1}{2}\alpha t^2 |
| 3rd equation of motion | v^2 = u^2 + 2ax | \omega^2_{2}=\omega^2_{1}+ 2 \alpha \theta |
| Kinetic energy | E=\frac{1}{2}mv^2 | E=\frac{1}{2}I\omega^2 |
| Momentum | P=mv | L=I\omega |
Here, u and v are the initial and final velocities respectively and a is the acceleration in linear motion. \color{Blue}\omega_{1} and \color{Blue}\omega_{2} are the initial and final angular velocity respectively and \color{Blue}\alpha is the angular acceleration.
This is all from this article on the rotation of an object about a fixed axis due to a Torque. If you still have any doubts on this topic you can ask me in the comment section.
Thank you!
Related posts:
3 thoughts on “Rotational motion of an object due to Torque”
Comments are closed.