Formula for Capacitance of a Capacitor – spherical, cylindrical

A Capacitor is one of the most useful circuit components. A capacitor can store electric charge or electric energy in it. The capacitor is nothing but a conductor or the combination of two conductors having equal and opposite charges. Then what makes the capacitor different from a conductor? What are the different types of capacitors? In this article, I’m going to explain all those things along with the definition, formula, unit, dimension for capacitance of a capacitor.

Contents in this article:

1. Difference between a Conductor and a Capacitor
2. General formula of capacitance of a capacitor
3. Definition for capacitance of a capacitor
4. Units and dimension
5. Graphs
6. On what parameters the capacitance depends?
7. Formula for capacitance of parallel plate capacitor
8. Capacitance of spherical capacitor
9. Capacitance of cylindrical capacitor
10. Use of a Capacitor

What is the difference between a conductor and a capacitor?

A conductor allows to flow electric charges through it to carry an electric current. It cannot store the electric charge or electrical energy in it. But if two conductors are placed at a small separation, the combination can store electric charges or electrical potential energy inside it. This combination of conductors is the Capacitor. The effect of a capacitor is known as the capacitance of the capacitor.

So, a capacitor is the combination of two equal and oppositely charged conductors placed at a small distance of separation. A capacitor can store electric charge and hence electrostatic energy. Sometimes, a single isolated conductor behaves like a capacitor. In this case, we consider that another similar conductor is present at infinity.

Formula for capacitance of a capacitor

If a conductor is charged, its electric potential increases. Thus, the electrostatic potential of a conductor is directly proportional to its charge. If the potential of a conductor becomes V due to its charge Q, then, \small V\propto Q

or, \small V=\frac{1}{C}Q

or, Q = CV………………. (1)

This is the general formula of capacitance of all types of capacitors. This is true for all types of capacitors. But there are some formulae for some specific types of capacitors like spherical capacitors, cylindrical capacitors, parallel plate capacitors, etc.

Definition of capacitance of a capacitor

The capacitance of a capacitor indicates its charge-storing capacity. More charge will rise the potential more and hence more potential energy. One can define the capacitance of a capacitor in terms of its charge and potential by using equation-(1).

The capacitance of a capacitor is defined as the amount of electric charge required to raise its electric potential by unity.

Units of Capacitance

The SI unit of capacitance is Farad (F) and the CGS unit of capacitance is Stat-Farad.

1 Farad = 9×10¹¹ Stat-Farad.

Practically used units are micro-Farad, nano-farad and pico-farad. Because the value of capacitance greater than this range is not possible to achieve on the Earth’s surface. why the capacitance of a capacitor cannot be in the range of 1 farad?

• 1 milli-Farad (mF) = 10^-3 Farad
• 1 micro-Farad (\small \muF) = 10^-6 Farad
• 1 nano-Farad (nF) = 10^-9 Farad
• 1 pico-Farad (pF) = 10^-12 Farad

Definition of 1 Farad Capacitance

One can establish the definition of one Farad from equation-(1). If 1 coulomb electric charge is required to raise the electric potential of a capacitor by 1 volt, then the capacitance of the capacitor is 1 Farad.

Dimension of Capacitance:

One can determine the dimensional formula of capacitance from equation-(1). Electric charge has the dimension of [TI] and the electric potential has the dimension of [ML²T^-3I^-1].

So, the dimensional formula for the capacitance is [M^-1L^-2T⁴I²].

C vs V, C vs Q, V vs Q Graphs for a Capacitor

One can get three graphs for a capacitor – Capacitance vs Charge graph (C-Q graph), Capacitance vs Voltage graph (C-V graph) and Voltage vs charge graph (V-C graph). Here, I am going to draw each graph one by one and will discuss the nature of all graphs. These variations of capacitance are valid for all capacitors.

Variation of Capacitance with the charge of capacitor

The capacitance of the capacitor is independent of the charge on its plate. Therefore, the Capacitance vs charge graph is a straight line with a constant value of capacitance.

Variation of capacitance with the voltage across it

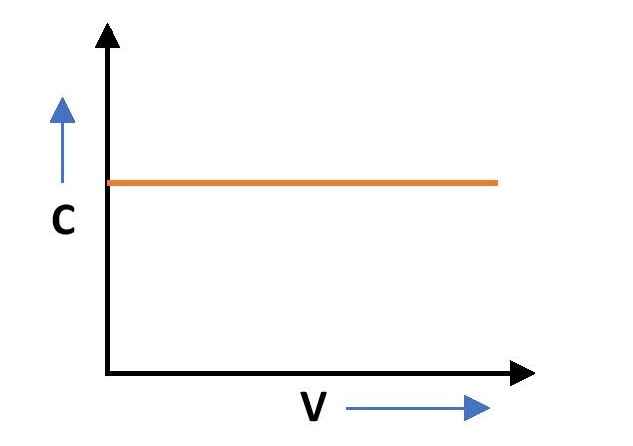
The capacitance of a capacitor is independent of the voltage across its plates also. Therefore, the capacitance versus voltage graph is similar to that of the capacitance vs charge graph. The nature of the C vs V graph is a straight line with a constant value of capacitance.

Variation of Voltage with the charge of a capacitor

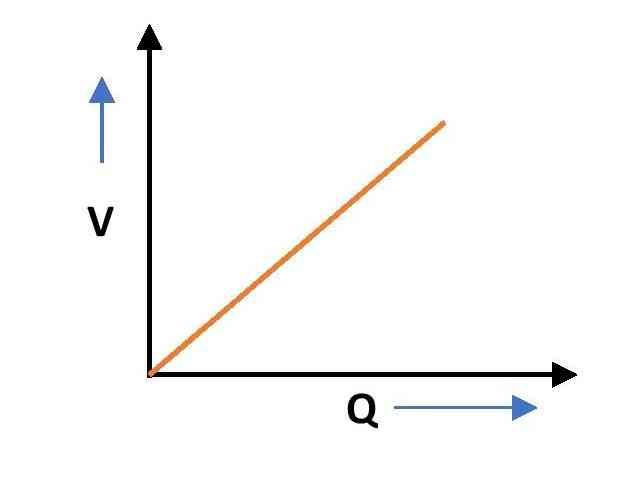
The variation of voltage of a capacitor with its charge can be observed from equation-(1). The voltage across the plates of a capacitor is directly proportional to the charge on it. Therefore, the Voltage vs charge graph gives a straight line passing through the origin. The slope of this graph is 1/C.

On which factors the Capacitance of a Capacitor depends?

The capacitance is the property of the capacitor. It does not depend on the amount of charge and the value of the applied voltage. The factors affecting the capacitance of a capacitor are –

1. Shape or the surface area of the conductors
2. Nature of the surrounding medium
3. Presence of other conductors
4. Distance of two conductors in the capacitor

The greater surface area allows to store of a greater amount of charges and hence the capacitance of the capacitor increases. The capacitance is inversely proportional to the distance between the conductors in a capacitor. The presence of an uncharged conductor near a capacitor increases its capacitance. If the surrounding medium is a dielectric medium, then the capacitance becomes greater.

What are the different types of Capacitors?

There are four different types of capacitors on the basis of their shapes. These are –

1. Single Isolated conductor
2. Parallel plate capacitor
3. Spherical capacitor
4. Cylindrical capacitor

For a single isolated conductor, it is imagined that there is another similar conductor at infinity. Hence, it is also a capacitor. A Spherical conductor is an example of an isolated conductor. The following section contains the formula for the capacitance of different types of capacitors.

Capacitance formula of an isolated spherical conductor

Let a spherical conductor of radius R and charge on its surface Q. Then electric potential on its surface is, \small {\color{Blue} V=\frac{Q}{4\pi \epsilon _{0}R}}

Then, capacitance, \small {\color{Blue} C=\frac{Q}{V}}

or, \small {\color{Blue} C=4\pi \epsilon _{0}R} ……… (2)

Thus, in SI system the capacitance of an isolated spherical conductor is, \small {\color{Blue} C=4\pi \epsilon _{0}R} and in CGS system the capacitance of the charged isolated conductor is equal to its radius (C = R). Thus the conductor with greater volume will have greater capacitance.

Suggested article: calculation of capacitance of Earth.

Formula for capacitance of a Parallel plate capacitor

A parallel plate capacitor consists of two parallel plates at some distance of separation. Plates can be rectangular or circular in shape. The plates should have equal and opposite charges on their surfaces.

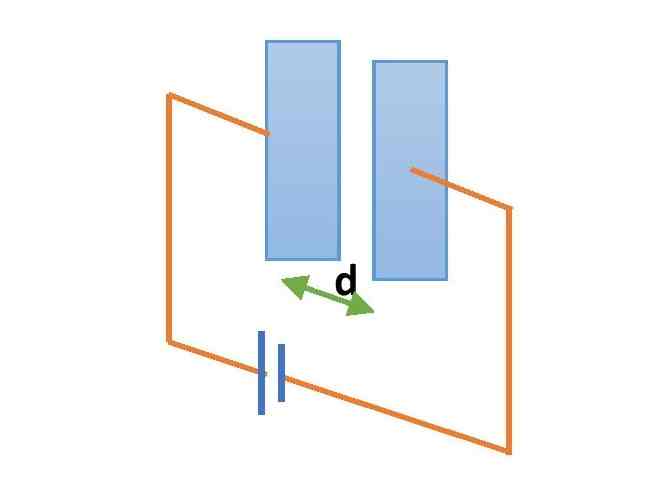
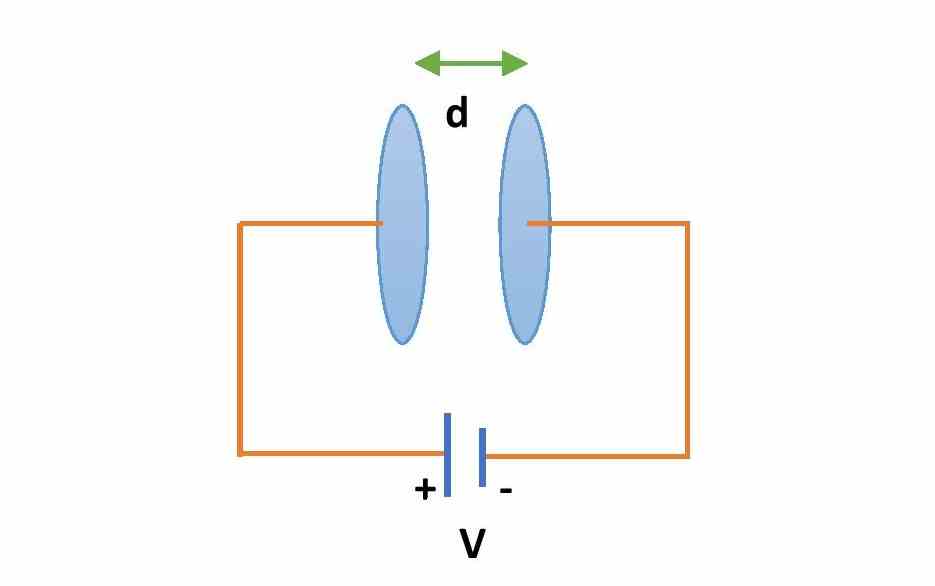
If A is the cross-section area of each plate and d is the distance between the plates, then the formula for capacitance of the parallel plate capacitor is,

\small {\color{Blue} C=\frac{k\epsilon _{0}A}{d}} …….(3) ( see the derivation of this formula)

where k is the dielectric constant of the medium between the plates and is the \small \epsilon _{0} permittivity of free space. If the medium between the plates is air medium, then the value of k is 1.

Formula for capacitance of a Spherical capacitor

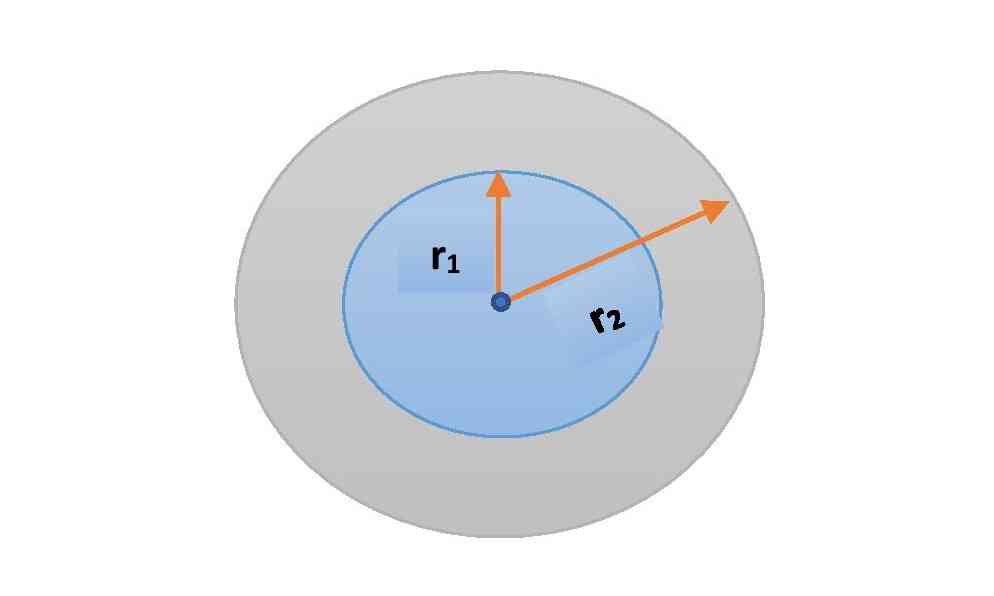
Two co-centric spherical conductors of different radii can act like a capacitor. Spheres should have equal and opposite charges. If r₁ and r₂ be the radii of the inner and outer spheres respectively, then the capacitance formula of the spherical capacitor is,

\small {\color{Blue} C=\frac{4\pi\epsilon _{0} r_{1}r_{2}}{r_{2}-r_{1}}} ………….(4)

Formula for capacitance of a Cylindrical capacitor

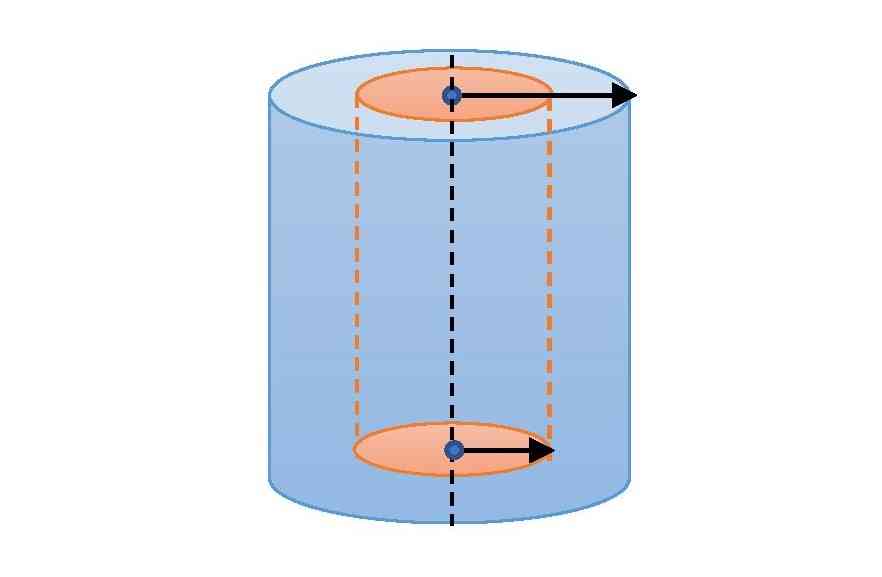
The system of two co-axial cylindrical conductors of the same length but different radii behave is also a capacitor. Let two co-centric cylinders have radii a and b respectively (b>a). Then the capacitance formula of the cylindrical capacitor is,

{\color{Blue} C=\frac{2\pi \epsilon _{0}}{ln\frac{b}{a}}} ………..(5)

Uses of a Capacitor

A capacitor is used as a circuit component for different purposes.

1. A capacitor can store electric charges and releases those charges the supplied voltage becomes less than the voltage across the capacitor. Therefore, an AC capacitor is useful in the rectifier circuit.
2. Capacitor can bypass alternating current (AC) through it. Because it offers low resistance to AC.
3. The main function of a capacitor is to block DC. These capacitors are known as DC-blocking capacitors.

This is all from this post on the capacitance formula of different types of capacitors. Hope this will help you in your study. If you have any doubt related to this topic, you can contact me over email.

Thank you!

Related Posts:

1. Parallel plate capacitor with dielectric medium
2. Energy stored in a Capacitor
3. Capacitance of Earth and other planets
4. Electric potential and potential energy
5. Gauss’s law of electrostatics
6. Electric field and electric field intensity