Combination of resistors in series and parallel connection

Suppose you have two carbon resistors of 2 ohms each, but you need 1 ohm resistance to connect in a circuit. What will you do if there are no other sources to collect a resistor of resistance 1 ohm? Again, what will you do if you need 4 ohms to use? Yes, we need to use a combination of the available resistors. There are two types of combinations of resistors – Series combination and Parallel combination. In this article, we are going to explain the combination of resistors in series and parallel circuits. Also, we will derive the equivalent resistance in series and parallel connections.

Contents in this article:

Series Combination of Resistors

Equivalent resistance of the combination of resistors in series
Parallel Combination of Resistors
Equivalent resistance for the combination of resistors in parallel

Numerical problems on the combinations of resistors

Combination of Resistors in series with circuit diagram

Circuit diagram for series combination of resistors — **Circuit diagram for a series combination of resistors**

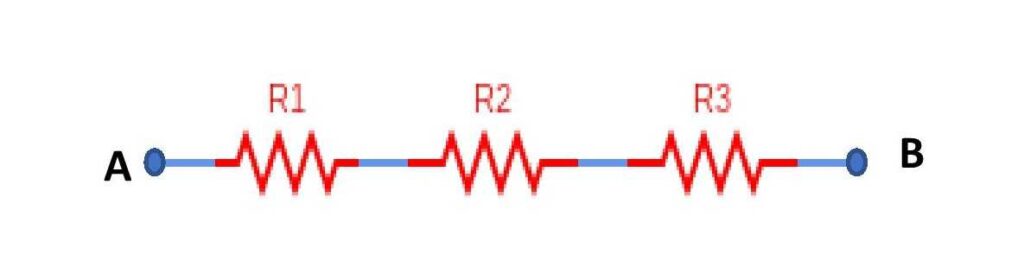
The neat circuit diagram for the series connection of resistors is shown above. In a series combination of resistors, we need to connect resistors one by one in a row. That means each resistor will be connected at the ending point of the previous one. The series combination of resistors has a significant role in electrical circuits. Using a series combination of resistors one can increase the effective resistance to a higher value. The connection of a battery across this combination will provide the current flow through the resistors.

Formula of equivalent resistance for a series combination of resistors

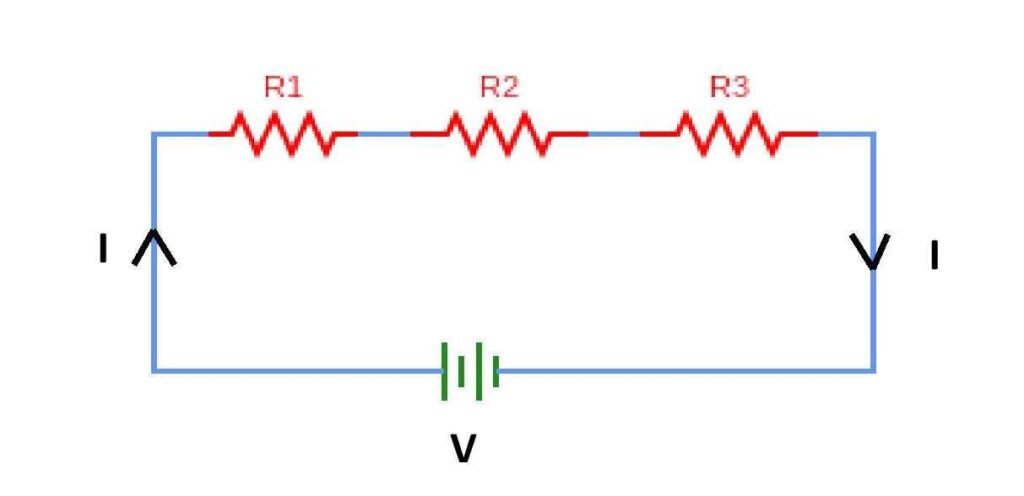
Let, three resistors of resistances R₁, R₂ and R₃ are connected in series and the battery across the series connection supplies the electric current through the circuit. Let, I be the electric current flowing through the circuit. Since, there is only one loop, then the same amount of current will flow through each resistance. Here, the battery supplies voltage across the resistors. If V₁, V₂ and V₃ be the voltage drops across the resistors R₁, R₂ and R₃, then

V = ( V₁ + V₂ + V₃ )

or, IR_eq = ( IR₁ + IR₂ + IR₃ ) [ Using Ohm’s Law]

or, R_eq = ( R₁ + R₂ + R₃ ) ………………….(1)

If we connect N number of resistors in series then the equivalent resistance of the series combination of resistors will be

R_eq = ( R₁ + R₂ + R₃ + ……. + R_N ) ……………..(2)

Equation-(2) gives the formula for equivalent resistance in series combination of resistors.

This equation shows that the effective resistance increases if we connect resistors in series. Series equivalent resistance is greater than every individual resistance in that combination.

Explain the Parallel combination of resistors with a neat diagram

Circuit diagram for parallel combination of resistors — **Neat circuit diagram for parallel combination of resistors**

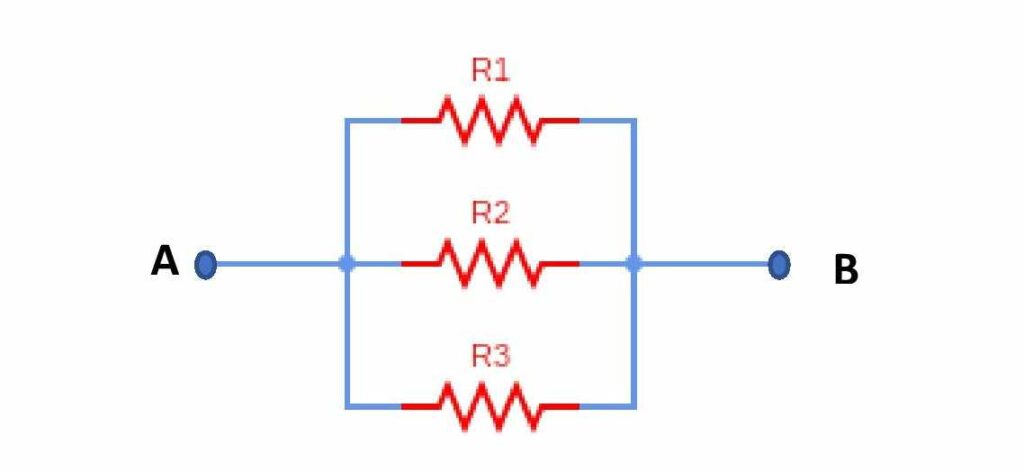
The neat circuit diagram for parallel connection of resistors is shown above. In a parallel combination of resistors, we need to connect resistors in a column between the same two points. The parallel combination of resistors also has a significant role in electric circuits. Using the parallel combination of larger resistors one can decrease the effective resistance to a lower value than individual resistors. The external battery will supply current through the resistors.

Derive the formula of equivalent resistance for the parallel combination of resistors

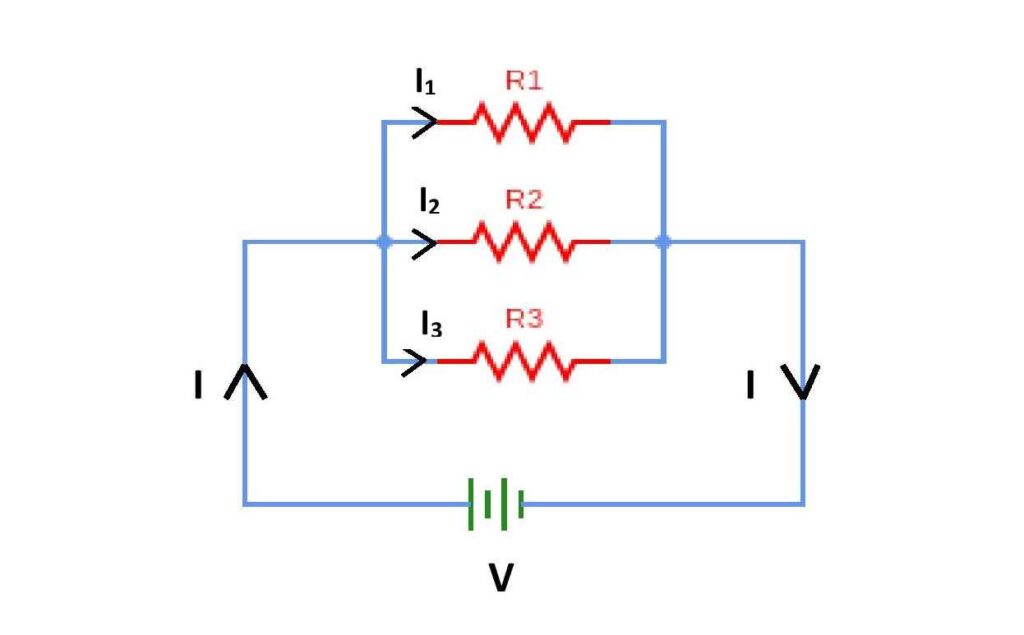
Let, three resistors of resistances R₁, R₂ and R₃ are connected in parallel and the battery across the parallel connection supplies the electric current through the circuit. As the resistors are connected parallelly across the same two points, then the voltage difference across all resistances is the same and is equal to the voltage of the external battery. Let, I be the electric current emitting from the battery. This current will divide into three parts to flow through three resistances. If I₁, I₂ and I₃ be the current through the resistors R₁, R₂ and R₃ then

I = ( I₁ + I₂ + I₃ )

or, $\small \frac{V}{R_{eq}}=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}$

or, $\small \frac{1}{R_{eq}}=(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}})$ ……………(3)

If we connect N number of resistors in parallel combination then the formula for equivalent resistance in parallel combination is

$\small \frac{1}{R_{eq}}=(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+.........+\frac{1}{R_{N}})$ ………………(4)

From equation-(4), one can see that the equivalent resistance in parallel combination is smaller than individual resistances of the combination. So, in parallel combination, the effective resistance decreases.

Facts related to the combination of resistors

The series connection of resistors increases the effective resistance and the parallel connection of resistors decreases the equivalent resistance.
Equivalent resistance of the series combination is greater than the individual resistances used in the combination. Thus, if we connect more resistances in series in a circuit, the amount of current flow decreases if the external voltage remains the same. Since there is only one path in a series connection, the amount of current flow through each resistor will be the same. But, the voltage drop across the resistors will be different.
The equivalent resistance of parallel combination is smaller than the individual resistances used in the combination. Thus, if we connect more resistances in parallel in a circuit, the battery will provide more current if the voltage remains the same. This amount of current divides into the branches of resistors. That means the current will not be the same through each resistor. As the resistors in parallel are connected between two same points, the voltage drop across all the resistors will be equal.

Numeral problems on combination of resistances

Two equal resistors are connected once in series and once in parallel combination. Find the ratio of equivalent resistances in these cases.
How can you get 3 ohm resistance by using three 2 ohm resistances?
Find the minimum effective resistance from the combination of four 2 ohm resistors.

This is all from this article on the combination of resistors in series and parallel and their derivation. If you have any doubt on this topic you can ask me in the comment section.

Thank you!

Related posts:

Impedance of L, C, LC, RLC circuit