Projectile Motion Equations in Physics

Equations for the linear motion and free fall are known to all. Using these equations one can find the position, velocity, acceleration and energy of a particle moving in a straight line with a constant velocity or constant acceleration. If we throw an object at an angle with respect to the ground, it will not follow a straight path. This type of motion of a projected particle is called the Projectile motion. Simple linear equations are not directly applicable for this motion. Then what are the equations of projectile motion? In this article, I’m going to derive and explain all the equations of projectile motion in physics.

Contents of this article:

What is projectile motion?

Examples of projectile motion.
How is the projectile motion difference from the straight line motion?
List of projectile motion equations.

Projectile motion graph
Derivation of physics equations of projectile motion.

What is projectile motion?

The Projectile motion is the motion of a particle thrown upward with an arbitrary angle with respect to the horizontal. The path or the trajectory of the projectile motion is not a straight line. The locus of projectile motion and its formula are discussed below.

Examples of projectile motion

Followings are the examples of projectile motion in real life –

The trajectory of a golf ball after playing the shot.
When a cricket player or baseball player throws a ball from the boundary, the ball follows projectile motion.

Javelin throw follows projectile motion
While firing a canon, the cannonball or round shot follows projectile path.

How is the projectile motion different from the free fall motion?

There is an obvious question that what are the differences between projectile motion and free fall? We have listed the differences between the projectile motion and free fall motion in below.

Free fall motion is one dimensional motion. But the projectile motion is two dimensional motion.
Free fall motion always occurs in straight line along vertically downward. But projectile motion is not a straight line motion. It follows parabolic path.
A particle falling freely under the gravity has an acceleration of 9.8 m/s². In projectile motion, the vertical motion has an acceleration which is same as the acceleration due to gravity but the horizontal motion does not have any acceleration.

List of equations of projectile motion in physics

Here are the formulae of projectile motion –

Maximum height, ${\color{Blue}H=\frac{u^{2} Sin^{2} \theta}{2g}}$
Total time of flight (until the particle falls down), ${\color{Blue}T=\frac{2u Sin\theta}{g}}$

Horizontal range, ${\color{Blue}R=\frac{u^{2} Sin2\theta}{g}}$

Where, u is the initial velocity and $\theta$ is the angle of projection with respect to the horizontal ground.

Projectile motion graph

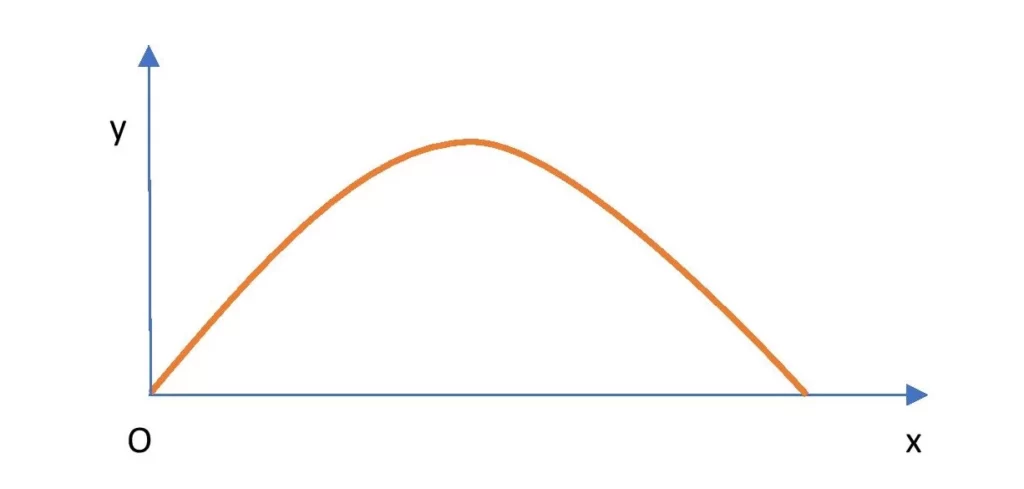
The locus or trajectory of a projectile is parabolic which is shown in the graph. Here, y gives the vertical distance (height) and x gives the horizontal distance (range).

Derivation of projectile motion equations

Let us consider, a particle is thrown with an initial velocity u in an angle $\theta$ with respect to the horizontal. The velocity of the particle will have two components –

Horizontal component of initial velocity is $ucos\theta$
Vertical component of initial velocity is $usin\theta$

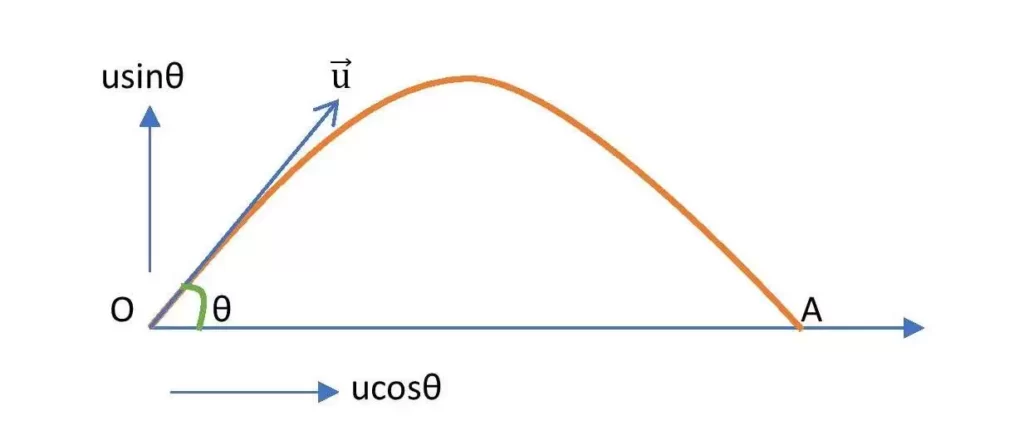
For vertical motion

At maximum height, the velocity of the particle will become zero. Using ${\color{Blue}v^{2}=(u^{2} - 2gH)}$ formula with v = 0 and initial velocity= $usin\theta$ , we get

The maximum height of the particle is, ${\color{Blue}H=\frac{u^{2} Sin^{2} \theta}{2g}}$ ……..(1)

Again, using ${\color{Blue}v=(u-gt)}$ formula with v = 0 and initial velocity= $usin\theta$ , we get

The time to reach the maximum height is, ${\color{Blue}t=\frac{u.Sin\theta}{g}}$ ……..(2)

This is the half of the total time of flight. It will take another t time to fall from maximum height to the ground.

So, total time of flight is, ${\color{Blue}T=2t=\frac{2u.Sin\theta}{g}}$ ……….(3)

For horizontal motion

Along the horizontal, the particle is moving with a uniform velocity, $ucos\theta$ . The particle will move for the time T. Then the horizontal range i.e. the horizontal distance travelled by the particle is, $\small{\color{Blue}R=ucos\theta. T}$

or, ${\color{Blue}R=\frac{u^{2} Sin2\theta}{g}}$ …….(4)

In this way we can derive all the formulae of projectile motion.

This is all from this article on the equations of projectile motion. If you have any doubts on this topic you can ask me in the comment section.

Thank you!

Related posts: