Kirchhoff’s law of current and voltage (KCL and KVL)

by

We already know that the Ohm’s law is a fundamental law in current electricity. But, Scientist Kirchhoff has given another two fundamental rules of electricity. With the help of these two rules one can easily find the current, voltage and resistance in an electrical circuit by using nodal analysis and loop analysis methods. In this article, we are going to discuss the Kirchhoff’s law of current and voltage, its mathematical form, applications and limitations.

Contents in this article:

  1. Kirchhoff’s current law (KCL)
  2. Kirchhoff’s Voltage law (KVL)
  3. Application of Kirchhoff’s law
  4. Limitation of Kirchhoff’s law

What are the Kirchhoff’s two rules?

  1. Kirchhoff’s current law (KCL) or Kirchhoff’s law of current
  2. Kirchhoff’s voltage law (KVL) or Kirchhoff’s law of voltage

These two rules of electricity are discussed below.

Kirchhoff’s law of current (KCL)

Statement of Kirchhoff’s current law(KCL)

Kirchhoff’s Current Law gives the relation between the currents passing through a junction point or node. This law states that the algebraic sum of the total current passing through (entering and leaving) a junction point is zero.

Explanation of KCL

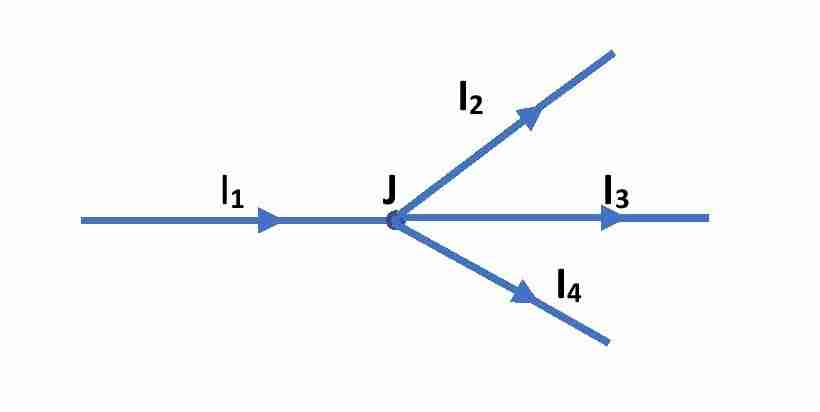
Circuit diagram to explain KCL
Circuit diagram to explain KCL

We consider a junction point J where four branches meet. Here, i1, i2, i3 and i4 are the four currents passing the junction point J via the four branches. Then according to Kirchhoff’s Current Law,

\sum i=0 …………….(1) This is the mathematical form of KCL.

Now, currents entering the junction point are the positive currents and the currents leaving the junction point are the negative currents. Then

or, i1– i2– i3-i4 = 0

  or,   i1= i2+ i3+ i4  …………. (2)

This equation shows that the amount of current entering the junction point is equal to the amount of current leaving that junction point.

KCL is consistent with law of conservation of electric charge

From the equation (2) one can see that the amount of current entering the junction point is equal to the total current leaving the junction point. Hence, amount of charge entering the junction point is equal to the total charge leaving the junction point. So, there is no accumulation of charges at the junction. Thus, Kirchhoff’s current law (KCL) is consistent with the law of conservation of charge.

Kirchhoff’s law of Voltage (KVL)

Statement of Kirchhoff’s voltage law (KVL)

KVL gives the relation between total EMF of the batteries and total voltage drops across the resistances in a closed circuit. This Law states that the algebraic sum of the total EMF in a closed loop is equal to the algebraic sum of the voltage drops across each resistances in the loop.

Explanation of KVL

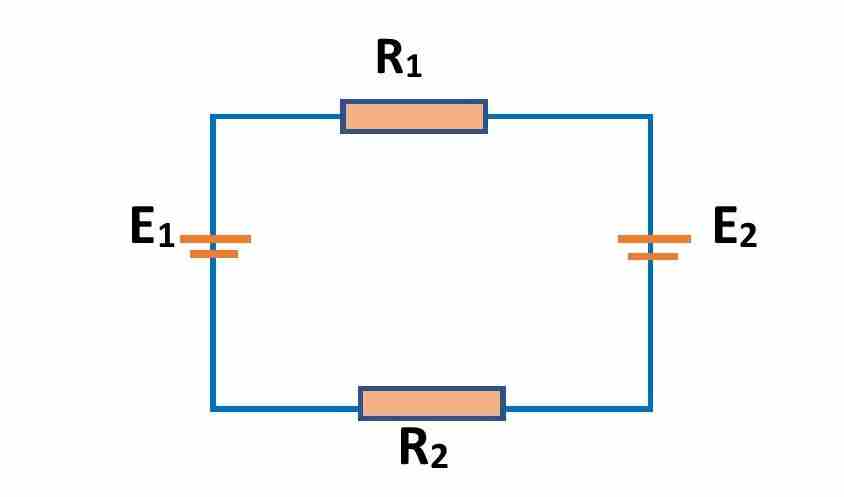
Circuit Diagram to explain KVL
Circuit Diagram to explain KVL

We consider a closed loop consisting of two batteries of EMFs E1 and E2 respectively (E1 >E2 ) and two resistances R1 and R2 respectively. Since, the batteries are connected in opposite polarities, the algebraic sum of the EMFs is (E1 – E2). If the current through the loop be I, then voltage drops across the resistances are V1=IR1  and  V2=IR2  respectively. Then according to Kirchhoff’s Voltage Law,

\small \sum E=\sum V

or, \small \sum E=\sum IR

or, (E1 -E2)=(IR1+IR2) ……………. (3)

This is the mathematical form of the KVL. This formula is very useful in nodal analysis.

KVL is consistent with law of conservation of electric Energy

If we multiply by I in both sides in equation-(3) then we get,

I(E1 -E2)=(I2R1+I2R2) …………….. (4)

So, the power delivered by battery is equal to the power consumed in resistances. Since, the electric power is defined the change in energy per unit time, then from equation-(4) one can say that the Kirchhoff’s voltage law is consistent with the law of conservation of energy.

Application of Kirchhoff’s laws

  1. KCL can be used to find the unknown current at any junction point.
  2. Using KVL one can determine the potential drop across a resistance.
  3. One can determine the current through any resistance or branch by using Kirchhoff’s laws.
  4. Another important use of KVL is to find the unknown resistance in a loop.

Limitations of Kirchhoff’s law

There are some limitations of Kirchhoff’s laws. These are –

  1. Kirchhoff’s law are not applicable in non-linear circuit where the non-ohmic circuit elements like diode, transistor etc. are used.
  2. Current flow produces electric field around the circuit. Also electrons in the circuit produce electric field around it. These electric and magnetic field may vary due to some causes. But while applying Kirchhoff’s law (KVL), it is assumed that electric and magnetic field around the loop is constant.
  3. Kirchhoff’s law (KVL) is not consistent with Faraday’s law of electromagnetic Induction as it do not consider the change in magnetic field during its application. If KVL includes the change in magnetic field around the circuit then there will be some loss in electric energy due to the induced EMF in the loop. Hence, some additional term will arrive in equation-(4) to satisfy the law of conservation of energy.

This is all from this article on KCL and KVL and the applications of KCL and KVL. If you have any doubt on this topic you can ask me in the comment section below.

Thank you!

Related Posts:

  1. Ohm’s law
  2. Ohm’s law experiment
  3. Electronic circuit components – use of capacitor, inductor, Resistor, diode etc.
  4. Series and parallel combination of resistors