Formula of Linear charge density & its calculation

by

A continuously charged conductor can have three types of charge densities. We already discussed surface charge density and volume charge density in other two articles. In this article, we’re going to discuss line charge density. Here you will learn the concept, definition and formula of linear charge density and how to calculate it.

Contents in this article:

  • Line charge distribution
  • What is linear charge density lambda?
  • Linear charge density formula
  • Unit of line charge density
  • Dimension of line charge density
  • How to calculate linear charge density?
  • How to find line charge density of a cylinder?

Line charge distribution

Linear Charge distribution
Linear Charge distribution

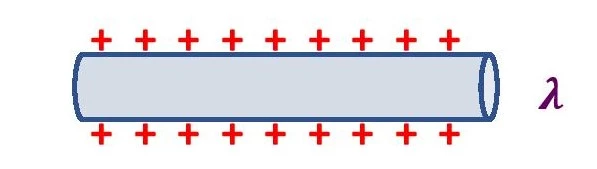
When the electric charge of a conductor is distributed along the length of the conductor, then the distribution of charge is known as the line distribution of charge. A charged conductor that has a length (like a rod, cylinder, etc.), has line charge distribution on it.

Linear charge density lambda

The linear charge density of a conductor is the amount of electric charge distributed per unit length of the conductor. It is denoted as the Greek letter lambda (\color{Blue}\lambda). It has another name line charge density.

Linear charge density formula

If a conductor of length L has total charge Q on it, then the formula of line charge density of the conductor is, \color{Blue}\lambda=\frac{Q}{L}……..(1)

This is the most general equation of linear charge density and is applicable to any linear conductor.

Unit of line charge density

The SI unit of line charge density (lambda) is Coulomb/meter (C.m-1) and CGS unit is StatC.cm-1.

Dimensional formula of line charge density

The dimension of electric charge [TI] and that of the length is [L]. So, the dimensional formula of the line charge density is [L-1TI].

Integral relation between total charge and line charge density

Let us consider a linear conductor of length L has the line charge density \lambda.

The amount of charge on an elementary length dl is, \color{Blue}dQ=\lambda.dl

Now, total charge on the conductor is, \color{Blue}Q=\int \lambda.dl……….(2)

This formula of line charge density is applicable only to a continuous body.

How to calculate linear charge density?

It is very easy to calculate the line charge density of a conductor. To do so, you just need to know the amount of charge on the conductor and the length of the conductor. After that, use the equation-(1) to find the line charge density lambda.

Using the same method, one can find the charge density of arc length also. In this case, it is better to take an elementary small length.

How to find linear charge density of a cylinder?

Here, we are going to understand the thing with the help of an example. Let, a cylinder of length 15 cm have a total charge of +2C on it. We want to find the line charge density of the cylinder.

So, the total charge, Q = 2C and length L = 15 cm = 0.15 m

Then, the line charge density of the cylindrical conductor is, \color{Blue}\lambda=\frac{2}{0.15}

or, \color{Blue}\lambda=13.33 C/m.

This is all from this article on the formula of linear charge density and its calculation. If you have any doubt on this topic can ask me in the comment section.

Thank you!

Related posts:

  1. Surface charge density
  2. Volume charge density
  3. Production of electric charge
  4. Continuous charge distributions