Expression for drift velocity of free electrons

If an external electric field is applied across a conductor, free electrons move in the conductor. The velocities of all the electrons are not the same at every point in the conductor. Therefore, we need to consider the average value of the velocities of the electrons. It is nothing but the drift velocity. In this article, we are going to discuss the definition and expression for drift velocity of free electrons in a conductor. This formula will give the relation between the drift velocity and electric current density. Also, we will derive an expression that relates the drift velocity with the relaxation time.

Contents of this article:

1. What is drift velocity?
2. Derive the expression for drift velocity of electrons in a conductor
3. Relation between drift velocity and current
4. Relation between drift velocity and electric field
5. Relaxation time and Drift velocity

What is the Drift velocity of free electrons?

Drift velocity of a free electron is defined as the average velocity of the electron with which it moves through a conductor or semiconductor to carry an electric current. We need to consider the average velocity of electrons because the velocity of an electron is not the same at every point in a conductor. Again, the velocity of every electron is different from other electrons at any time and at any point in the conductor.

Expression for drift velocity

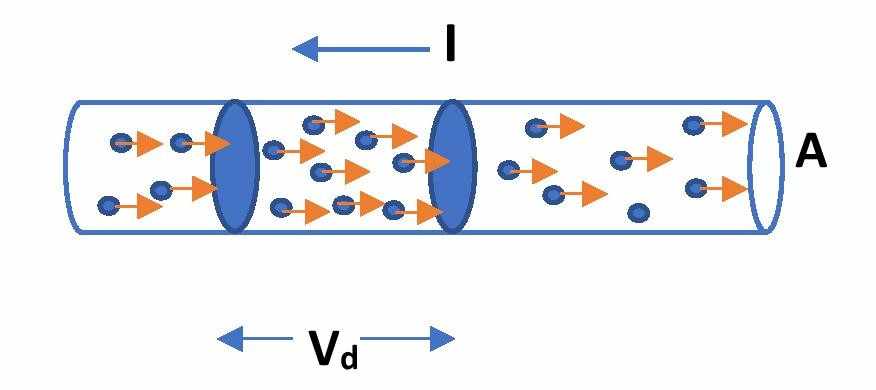
Let electrons are moving through a current-carrying wire of current I. This wire can be considered as a cylinder of cross-section area A. We consider that n number of electrons of charge e is moving per unit volume of the wire with the drift velocity V_d. Since V_d is the drift velocity, it implies that the electrons move V_d length of the wire per unit time. So, the volume of occupation of the electrons per unit time is AV_d.

So, the total number of electrons crossing the volume AV_d per unit time is \color{Blue} N = nA V_{d}

Now, each electron has the charge of e. So, the amount of electric charge crossing the volume per unit time is \color{Blue} eN = enV_{d}

Since the amount of charge flowing per unit time is the electric current then the electric current through the wire is, \color{Blue} I = enV_{d}.

or, the drift velocity of free electrons, \color{Blue}V_{d} = \frac{I}{enA}………………… (1)

This is the relation between drift velocity and current.

Again, the current per unit area is the current density (J). So, J = I/A.

So, another expression for drift velocity of electrons in a wire is, \color{Blue}V_{d} = \frac{J}{en}……………… (2)

en is the charge density. So, one can use \small {\color{Blue} \rho =en} in equation (1) and (2).

Unit of drift velocity of electrons

The units of drift velocity are the same as the unit of normal velocity. The SI unit of drift velocity is m/s and CGS unit of drift velocity is cm/s.

Relation between drift velocity and current

The relation between drift velocity and electric current is, \color{Blue}V_{d} = \frac{I}{enA} or, \color{Blue} I = enA V_{d}

Again, charge density, \small \color{Blue}\rho=en . Then, the relation between drift velocity and electric current is, \small \color{Blue} I= \rho A V_{d}.

Relation between drift velocity of electrons and electric current density

current density, J = I/A

Then the relation between drift velocity and current density is, \color{Blue}V_{d} = \frac{J}{en} or, \color{Blue} J = enV_{d}

Again, en is the charge density. So, \small J = \rho V_d. This is the relation between the current density and charge density.

Relation between drift velocity and electric field

From the differential form of Ohm’s law, we get the relation between the current density and electric field is \small J = \sigmaE

Then, from above relation, \small\sigmaE = enV_d or, drift velocity, V_d = \small\frac{\sigma}{en}E

Again, Mobility, \small\mu=\frac{\sigma}{en}

Then, the relation between the drift velocity, electric field and the mobility of electron is, V_d = \small\muE

Relation between drift velocity and relaxation time

Relaxation time is the average time interval between the two successive collisions of an electron with other electrons during their motion in the conductor.

If a voltage V is applied across a conducting wire of length L, then electric field E = V/L will appear inside the conductor. Let an electron of charge e (magnitude) is moving under the electric field E. Then the electric force on the charge is F = eE.

If m is the mass of the electron then the acceleration of the electron is, a = F/m = eE/m

Now, if t is the relaxation time then the average velocity of electrons between two successive collisions or the drift velocity of electrons is,

V_d = at

or, drift velocity, V_d = eEt/m ……………… (3)

This is the relation between the drift velocity of electron and the relaxation time.

This is all from this article on the expression for drift velocity of electrons in a conductor. If you have any doubts on this topic you can ask me in the comment section.

Keep visiting for more articles.

Thank you!

Related Posts:

1. Ohm’s law
2. Mobility of electron and holes
3. Kirchhoff’s law (KCL and KVL)