Electrostatics Article – 7
Let a source charge Q produces an electric field E and a positive test charge q is placed at a distance r from the source charge. Coulomb’s law gives the expression for the electrostatic force on the positive charge q due to the source charge Q. Now, if we want to move the test charge towards the source charge i.e. in the opposite direction of the electrostatic force, external work is required. This work is stored as the electrostatic potential energy which we have discussed in another article. If the test charge is a unit positive charge, then the work done is known as the electrostatic potential instead of the electrostatic potential energy.
In this 7th article on electrostatics, I’m going to explore the concept of electrostatic potential and potential difference, its formula, units and dimension. Also, we will derive the expression for electric potential due to a point charge.
Definition of electrostatic potential
The electrostatic force between two positive charges acts in the outward direction. Therefore, to move a test charge towards the source charge external work is to be done. Electrostatic potential at a point inside an electric field is defined as the amount of work done in bringing a unit positive charge from infinity to that point. Another name for electrostatic potential is electric potential.
Electric potential is a scalar quantity.
Electrostatic potential formula
The formula of electric potential at distance r from a point charge Q is \small {\color{Blue} V=\frac{Q}{4\pi \epsilon_{0}r}}. This formula is not the same for all the conductors. Equations of electric potential are different for the different shaped conductors. The above formula is applicable for a point near a point charge and for a point outside a spherical conductor.
Units of electric potential
- SI unit of electric potential is Volt
- CGS unit of electric potential is Stat-Volt.
- One Stat-volt is equal to 300 Volts.
Dimension of electric potential
The dimensional formula for the electric potential is [ML2T-3I-1].
One can determine the dimension of the electric potential from the formula of the electric potential energy, W = qV. Where W is the work done, q is the electric charge and V is the electric potential.
Derivation of the formula for electric potential due to a point charge
We consider a point charge Q produced an electric field around it. We want to find the work done in bringing a unit positive charge from infinity to a point P at r distance from the charge inside this field region. This gives the electric potential at that point.
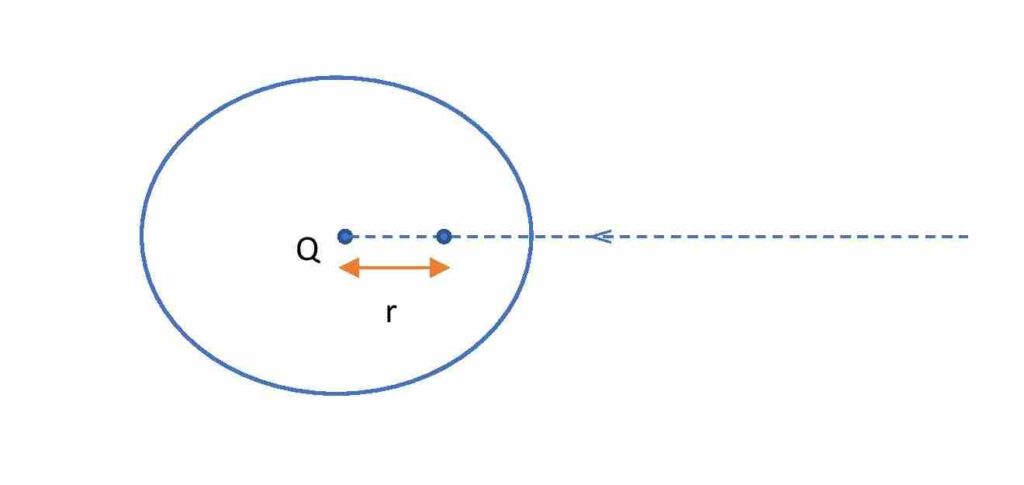
Let, at any instant the unit positive charge is at a distance x from the Q inside the electric field. Then electric force on the unit charge at that point is, \color{Blue}\small \frac{Q}{4\pi \epsilon _{0}x^{2}}.
Now, the work done in moving the charge for dx distance is, dW=\small \vec{F}.d\vec{x}.
Here, the electric force is in the outward direction and the displacement occurs in the inward direction. So, the angle between the electric force and the displacement is 180 degrees.
Then, dW = F.dx.cos180°
or, \color{Blue}dW= -\small \frac{Q}{4\pi \epsilon _{0}x^{2}}dx
Then, the total work done in bringing the unit positive charge from infinity to r distance is, W=\small \int dW
or, \color{Blue}W=\small \frac{Q}{4\pi \epsilon _{0}}\color{Blue}\small \int_{\infty }^{r}\frac{dx}{x^{2}}
or, \color{Blue}W=\small \frac{Q}{4\pi \epsilon _{0}r}…………….(1)
This work done on the unit positive charge is renamed as the electric potential. Equation-(1) gives the expression for electric potential at r distance from a point charge Q.
So, the electric potential, \color{Blue}V=\small \frac{Q}{4\pi \epsilon _{0}r}…………(2)
This is the electric potential equation for a point charge.
What is Electrostatic potential difference?
The definition is visible in its name. The difference in the electric potential between two points in an electric field is the electrostatic potential difference between these two points. If VA and VB be the electric potentials at points A and B respectively, then the electric potential difference between these two points is VAB = (VA-VB).
Relation between electric field and electric potential
From the equation-(2), we get the electric potential at r distance from a point charge Q is \color{Blue}V=\small \frac{Q}{4\pi \epsilon _{0}r}. Again, the electric field at that point is, \color{Blue}E=\small \frac{Q}{4\pi \epsilon _{0}r^{2}}.
Then, V = Er in terms of the magnitude of the electric field and distance.
In vector form, \color{Blue}V=\small \vec{E}.\vec{r} ………..(3)
The dot product between the electric field and displacement vector gives the electric potential.
Now, from the concept of the electric potential, we became to know that the electric charge is displaced in opposite direction to the electric field. So, the angle between E and r is 180 degrees.
So, V = – E.r
In the integral form, \color{Blue}V=\small \int \vec{E}.d\vec{r}= \color{Blue}\small -\int E dr…………(4)
In the differential form, \color{Blue}E=\small -\frac{\mathrm{d} V}{\mathrm{d} r}………(5)
Equation-(4) and (5) are the most popular equations of electric potential which relate it to the electric field intensity, E.
This is all from this article on electrostatic potential and potential difference. If you still have any doubts on this topic you can ask me in the comments.
Thank you!
Related posts:
