Newton’s second law of motion with example

by

The three famous laws of motion given by sir Isaac Newton are the basic laws in classical mechanics. These laws describe the rest and motion states of an object. We already have explained Newton’s first law of motion and its importance. In this article, I’m going to explain Newton’s second law of motion with example and its importance. Also, I’ll show how to derive the equation or the formula of force from Newton’s second law of motion.

Contents of this article:

  1. Definition or statement of Newton’s second law of motion
  2. Examples of Newton’s 2nd law of motion
  3. Explanation of Newton’s 2nd law of motion
  4. Importance of Newton’s second law of motion
  5. Equation of Newton’s second law of motion
  6. Derivation of the formula for force from Newton’s second law

Definition of Newton’s second law of motion

Here, the term definition refers to the statement. Newton’s second law of motion states that the rate of change in momentum of a body over time is directly proportional to the net force applied to it and the change in momentum occurs in the same direction as the net applied force.

All the considerations are made for a linear motion and the mentioned momentum is actually the linear momentum. However, we can use this law in rotational motion too. But in the case of rotational motion, we need to do all the calculations for small paths of the entire curved trajectory. Because a small portion of a curve is almost a straight line.

Explanation of Newton’s second law of motion with example

Image source: by Chris Thornton from Pixabay

The cart is moving as the kid is pushing it

From the statement of Newton’s second law of motion, it is clear that an applied force to a body causes the motion of the body if the body is initially at rest and the velocity of the body increases if the body is initially in motion. Since the velocity of the body is changing in either case, it should have an acceleration due to this applied force.

So, according to Newton’s second law of motion,

  1. A resting body can be moved by applying a net external force to it. But any amount of force cannot move the body. Because in practical cases there exist a static friction force on all the objects. So, the amount of applied force must be greater than the static friction force or any other opposition force.
  2. The velocity of a moving object can be changed (increase or decrease) by applying an external force. If the force is applied in the direction of its motion then its velocity increases and if the force is applied against its motion then its velocity decreases.
  3. In both cases, the linear momentum of the object changes with respect to time. That means the object will have acceleration or retardation when an external force acts on it.

Examples for Newton’s 2nd law

The cart is moving as the man is pulling it

According to the statement of Newton’s second law of motion, a rest body will move after applying a net force on it. Again, a moving body will move faster if a force is applied along its motion and the velocity of the body will slow down if the applied force acts in the opposite direction of its motion.

Examples of Newton’s second law of motion in daily life:

  1. Riding a bicycle. Here, the legs of the rider provide the external force on the paddle of the bicycle and thereby its velocity increases i.e. an acceleration arises. Again, when the rider applies the break (an external force against the motion) of the bicycle, its velocity decreases because of arising retardation.
  2. Golf players apply external force on a ball by hitting the ball with their sticks to move the golf ball towards a hole.
  3. During traveling, we carry our trolley bags by pulling (a force) its handle.
  4. Kid rolls a marble on the floor by pushing (a force) the marble.

Equation of Newton’s second law of motion

If dP be the change in momentum in the time dt, then the rate of change in momentum is \small \frac{dP}{dt}. Then according to the Newton’s second law of motion, \small {\color{Blue} F\propto \frac{dP}{dt}}

The mathematical equation for Newton’s second law of motion is \small {\color{Blue} F= \frac{dP}{dt}}………….(1)

Here, the proportional constant is considered to be unity for an object of unit mass and unit acceleration due to unit applied force.

Now equation-(1) has different forms depending upon the nature of mass and velocity.

Formula of Newton‘s second law of motion for constant mass and changing velocity:

When the mass of the object is constant and its velocity is varying, then the equation for Newton’s 2nd law of motion is, \small {\color{Blue} F= m\frac{dV}{dt}}…………….(2)

Again, the rate of change in momentum is the acceleration (a) of the body. Then, Newton’s equation of motion, F = ma……….(3)

This formula is frequently used in the case of motion of all classical particles.

Formula of Newton’s second law of motion for varying mass:

Variable mass system: Motion of a Rocket

For a variable mass system, both the mass and the velocity of the object vary. Then the equation of Newton’s second law of motion becomes as \small {\color{Blue} F= (m\frac{dV}{dt} - u\frac{dm}{dt})}………………(4)

Where u is the exhaust velocity of the system.

The motion of the rocket is an example of variable-mass system. In this system, the exhaust velocity is the velocity of escaping the mass of fuel relative to the rocket.

Importance of Newton’s 2nd law

  1. From Newton’s second law of motion one can get the equation of force. Using that equation one can calculate the magnitude of applied force on a body after observing its mass and acceleration.
  2. One can control the acceleration of an object by controlling the applied force on that object.

Derivation of formula for Force from Newton’s 2nd law

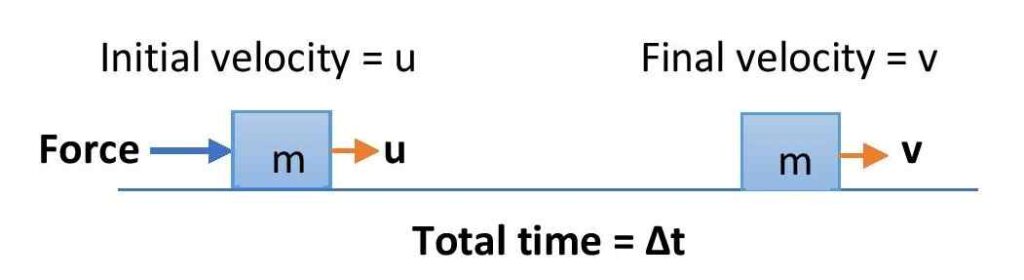
Let an object of mass m is moving with its initial velocity u. Now, an external force F is applied on the object and thereby after a time interval ∆t its velocity becomes v.

So, the change in velocity of the object, ∆v = (v-u)

Then, the change in linear momentum of the object is, ∆P = m(v-u)

Then, according to Newton’s second law of motion, \small {\color{Blue} F\propto \frac{\Delta P}{\Delta t}}

or, \small {\color{Blue} F=K\frac{m(v-u)}{\Delta t}}…………….(5) Where, K is proportional constant.

Now, the acceleration of the object is, \small {\color{Blue} a=\frac{v-u}{\Delta t}}

Then, from equation-(5) we get, \small {\color{Blue} F=Kma}…………..(6)

Now, if an object of unit mass gains unit amount acceleration due to the application of unit mount of force, then the proportional constant K=1.

Then, the mathematical formula of Newton’s second law of motion is \small {\color{Blue} F=ma}……………(7)

This is the proof of Newton’s equation F = ma.

This is all from this article on Newton’s second law of motion with example and its explanation. If you have any doubts on this topic you can ask me in the comment section.

Thank you!

Related posts:

  1. Newton’s first law of motion
  2. Proof of Newton’s first law from second law
  3. Newton’s third law of motion
  4. Fourth law of motion by Newton
  5. Momentum and Impulse
  6. Projectile Motion
  7. Equations of Force in Physics