In the previous article, I explained the capacitance of different types of capacitors. A parallel plate capacitor is one of the most popular capacitors and it has wide applications in electrical circuits. In this article, I’m going to explore the capacitance of a parallel plate capacitor and its behavior in presence of a dielectric medium or slab between its plates.
Contents in this article:
- How to construct a Parallel plate capacitor?
- Formula for capacitance of parallel plate capacitor.
- Derivation of Capacitance of a parallel plate capacitor.
- On which parameters does the capacitance of parallel plate capacitor depend?
- Capacitance of parallel plate capacitor with dielectric medium.
- Uses of parallel plate capacitor.
How to construct a Parallel plate capacitor?
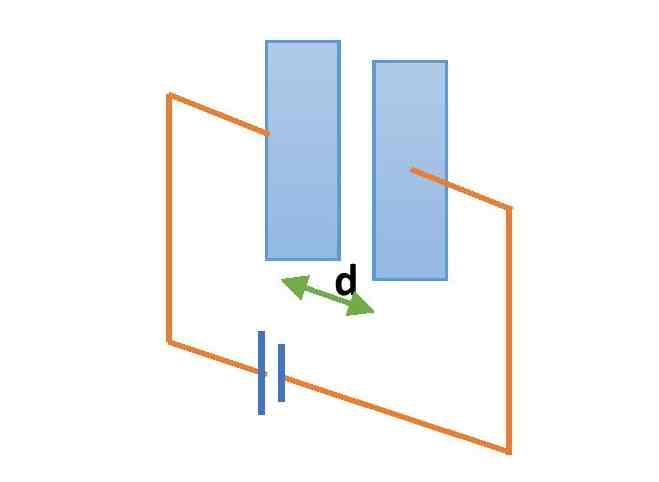
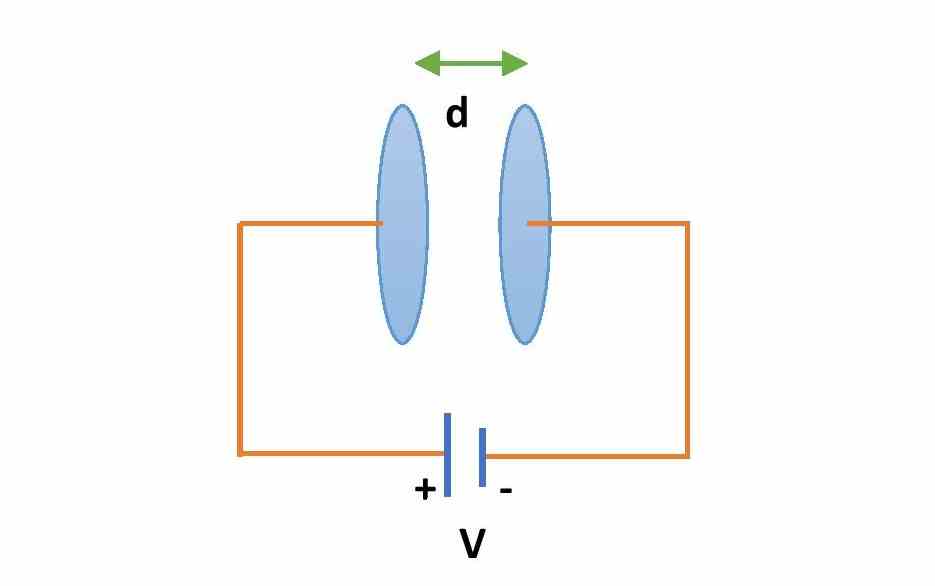
A parallel plate capacitor is a system of equally and oppositely charged two conductors placed at some distance of separation. To construct a parallel plate capacitor we need to place two conducting plates at a small separation. The plates should be equally and oppositely charged. The shape of the plates can be rectangular or circular.
Formula for capacitance of parallel plate capacitor
The general formula for any type of capacitor is, Q = CV, where Q is the electric charge on each plate, V is the potential across the plates and C is the capacitance of the capacitor.
Now, a parallel plate capacitor has a special formula for its capacitance. If the cross-section area of each plate is A and the distance between the plates is d, then the formula for capacitance of the parallel plate capacitor is, \small {\color{Blue} C=\frac{\epsilon _{0}A}{d}}
If the space between the plates is filled with a dielectric medium of dielectric constant K then from the above formula, \small {\color{Blue} C=\frac{K \epsilon _{0}A}{d}}.
This is the formula for the capacitance of a parallel plate capacitor with a dielectric slab.
Derivation of Capacitance of a parallel plate capacitor
Let us consider a parallel plate capacitor with two plates of cross-section area A, separated by a distance d. The medium between the plates is air medium. If V is the voltage applied across the plates of the capacitor, then the electric field inside the capacitor will be, \small {\color{Blue} E=\frac{V}{d}} ……………..(1)
Again, from Gauss’s law of electrostatics, one can get the electric field inside a capacitor of two oppositely charged plates is, \small {\color{Blue} E=\frac{\sigma }{\epsilon _{0}}} …………….(2)
Where \small {\color{Blue} \sigma } is the surface charge density of each plate.
From equation-1 and equation-2 we get, \small {\color{Blue} \frac{V}{d}}={\color{Blue} \frac{\sigma }{\epsilon _{0}}}
or, \small {\color{Blue} V}={\color{Blue} \frac{\sigma d}{\epsilon _{0}}}
or, \small {\color{Blue} V}={\color{Blue} \frac{Q d}{\epsilon _{0} A}}
Since, the surface charge density, \small \sigma =\frac{Q}{A}
Now, the capacitance of the parallel plate capacitor is, \small {\color{Blue} C=\frac{Q}{V}}
or, \small {\color{Blue} C=\frac{\epsilon _{0}A}{d}} ……………………(3).
This is the parallel plate capacitor formula without the dielectric.
Now, if a dielectric medium of dielectric constant K is inserted in the region between the plates then the parallel plate capacitor formula with dielectric will be as, \small {\color{Blue} C=\frac{K \epsilon _{0}A}{d}}.
On which factors does the capacitance of parallel plate capacitor depend?
From equation-3 one see that the capacitance of a parallel plate capacitor depends on the following parameters –
- The cross-section area of the plates. A Greater cross-section area gives a greater value of capacitance.
- Distance between the plates. Capacitance is inversely proportional to the distance between the plates.
- The medium between the plates. The presence of a dielectric medium between the plates increases the capacitance of the capacitor.
Capacitance of parallel plate capacitor with a dielectric medium
Let a parallel plate capacitor with plate area A and the distance between the plates d.
When the medium between the plates is air medium, the capacitance, \small {\color{Blue} C=\frac{\epsilon _{0}A}{d}}.
And, when a dielectric slab of dielectric constant K is inserted between the plates, the capacitance, \small {\color{Blue} C=\frac{K\epsilon _{0}A}{d}}.
So, the capacitance of a parallel plate capacitor increases due to inserting a dielectric slab or dielectric medium between the plates of the capacitor. The new value of the capacitance becomes K times the capacitance when the medium between the plates is air.
Effects on capacitance, charge and voltage due to inserting the dielectric slab
- Due to the insertion of the dielectric slab the capacitance of the capacitor increases.
- If the capacitor is in charging mode i.e. if the battery is on, then the voltage across the capacitor remains the same and hence the amount of charge on each plate increases. But if the battery is off, then the charge on the plates remains the same and the voltage across the plates decreases to maintain the Q = CV formula.
Uses of a capacitor
AC Capacitors and DC-blocking capacitors have huge applications in our daily life. Ceiling fans, TVs and other electric devices use dc capacitors for different purposes. An AC capacitor can be used in a filter circuit. Overall, the capacitor is one of the most useful circuit components.
Homework Problems:
- A parallel plate capacitor has d = 2 mm and A = 5 cm2. If the medium between the plates is air medium and 10 volt voltage is applied across the capacitor then find the electric charge of the capacitor. Now, if you insert a dielectric slab (K=2) then what will be the charge of the capacitor?
- Suppose you have inserted a dielectric slab (K=3) between the plates of a parallel plate capacitor of capacitance C. What will be the ratio of the new capacitance to the previous capacitance of the capacitor?
This is all from this article on the parallel plate capacitor with dielectric slab. If you have any doubt on this topic you can ask me in the comment section.
Thank you!
Related posts:
- Capacitance of different type of capacitors – Spherical, Cylindrical, parallel plate and isolated conductors.
- Energy stored in a capacitor
- Capacitance of Earth and other planets.
- Voltage drop across a capacitor
- Surface charge density of a capacitor
Comments are closed.