Formula for moment of Inertia of different shapes

The term Moment of inertia is used in physics to describe the rotation of an object. The moment of inertia has the same mathematical role in rotational motion as that of the mass in linear motion. But the physical significance of the moment of inertia is different from that of the mass of an object. In this article, we’re going to discuss the formula for the moment of inertia for different shapes like a ring, disk, sphere, rod, etc.

Contents in this article:

1. Definition of moment of inertia
2. Mathematical equations of moment of inertia
3. Units of moment of inertia
4. Dimension of moment of inertia
5. Physical significance of moment of inertia
6. Moment of inertia and mass
7. Equation for moment of inertia for different objects list

Definition of Moment of Inertia

In linear motion, a force produces acceleration in a body. But the rotational motion arises due to the presence of a Torque. A torque can rotate an object and produces angular acceleration in that object. The moment of inertia of a rotating object is defined as the amount of external torque required to produce a unit amount of angular acceleration in that object.

Sometimes, the moment of inertia is defined as the multiplication between the mass of the object and the square of the distance of the object from the axis of rotation. But this is not the 100% correct definition. It can be used to solve numerical problems.

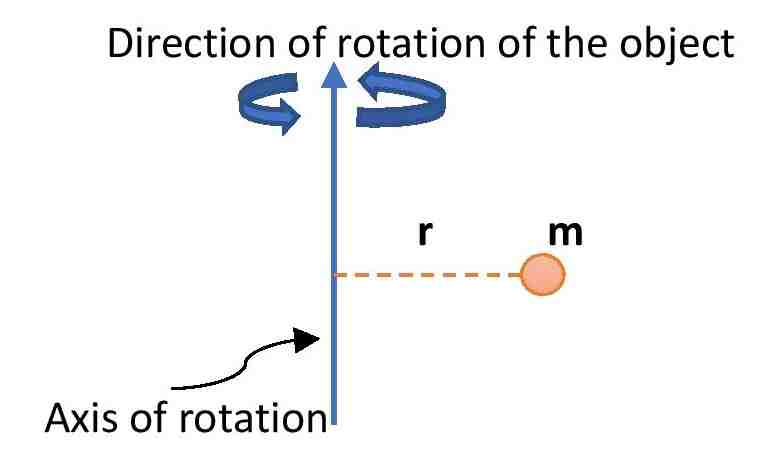
Moment of inertia is a tensor quantity. But in lower classes, it is considered to be a scalar quantity. The symbol of the moment of inertia is I. It depends on the mass of the object and the distance of the object from the axis of rotation. The values of the moment of inertia of the same object are different for different axes of rotations. Another name for the moment of inertia is the moment of rotation.

The general equation for Moment of inertia

There are two mathematical equations for moment of inertia. These are –

\small {\color{Blue} I = mr^{2}} ……….(1)

Where m is the mass of the object and r is the distance of the object from the axis of rotation. This is the most common formula for moment of inertia.

And, \small {\color{Blue} \tau = I\alpha } ……….(2)

Where \small {\color{Blue} \tau } is the Torque on the object and \small {\color{Blue} \alpha } is the angular acceleration of the object. This equation is used to define the moment of inertia.

Unit of Moment of Inertia

One can easily derive the units of moment of inertia from the equation-(1). The SI unit of moment of inertia is kg.m² and the CGS unit of moment of inertia is g.cm².

Dimension of Moment of Inertia

To find the dimensional formula of moment of inertia, we will use the equation-(1) again. The dimension of moment of inertia is [ML²].

Physical Significance of Moment of Inertia

Moment of inertia is the rotational counterpart of the mass. Physically, the moment of inertia represents the amount of external torque is required to produce a unit amount of angular acceleration in an object. This gives an idea of how easily an object can be rotated.

Is there any relation between Moment of Inertia and Mass?

The moment of inertia is the rotational counterpart of the mass of an object. Mathematically, it plays the same role in rotational motion as the mass plays in linear motion.

For example, in linear motion F = ma, where m is the mass of the object, F is the force that causes the linear motion and a is the linear acceleration. Now, in rotational motion, \small {\color{Blue} \tau = I\alpha }, where, I is the moment of inertia, \small {\color{Blue} \tau } is the torque that causes rotational motion and \small {\color{Blue} \alpha } is the angular acceleration.

The comparison between these two equations concludes that the Moment of inertia has the same role in rotational motion as that of the mass in linear motion.

Formula for Moment of inertia of different shapes

Here is a chart or list of the moment of inertia for different shapes like a rod, circle or circular ring, disk, sphere, cylinder, etc. about different axes of rotation.

Serial No.	Shape of the Object	Axis of Rotation	Expression for Moment of Inertia
1	Uniform Rod	Axis is perpendicular to the length of the rod and passing through one of its ends	\small I=\frac{1}{3}ML^{2}
2	Uniform Rod	Axis is perpendicular to the length of the rod and passing through the center of mass of the rod	\small I=\frac{1}{12}ML^{2}
3	Circle or circular ring	Axis is perpendicular to the plane and passing through the center of mass of the ring	\small I=MR^{2}
4	Circle or circular ring	About the diameter of the ring	\small I=\frac{1}{2}MR^{2}
5	Uniform Disk	Axis is perpendicular to the plane and passing through the center of mass of the disk	\small I=\frac{1}{2}MR^{2}
6	Uniform Disk	About the diameter of the ring	\small I=\frac{1}{4}MR^{2}
7	Hollow Sphere	About its diameter	\small I=\frac{2}{3}MR^{2}
8	Solid Sphere	About its diameter	\small I=\frac{2}{5}MR^{2}
9	Hollow Cylinder	About its own axis	\small I=MR^{2}
10	Hollow Cylinder	About the axis perpendicular to its length and passing through the center of mass	\small I=\frac{1}{12}ML^{2} + \frac{1}{2}MR^{2}
11	Solid Cylinder	About its own axis	\small I=\frac{1}{2}MR^{2}
12	Solid Cylinder	About the axis perpendicular to its length and passing through the center of mass	\small I=\frac{1}{12}ML^{2} + \frac{1}{4}MR^{2}

Here, L is the length of the rod and cylinder, R is the radius of the circle or ring, disk, sphere and cylinder and M represents the mass of each object. These parameters L, R and M do not have equal values in each body. While calculating the M.O.I., you need to consider the values accordingly.

Some important questions

1. On which parameters the moment of inertia depends? Answer: Moment of inertia depends on the mass of the object, Axis of rotation of the object and the distance of the object from the axis of rotation.
2. Is moment of inertia a scalar quantity or vector quantity? Answer: Moment of inertia is a Tensor quantity. But in junior classes, it is considered a scalar quantity.

This is all from this article on the moment of inertia and its formula for different shapes. If you have any doubts on this topic you can ask me in the comment section.

Thank you!

Related Posts:

1. Rotational kinetic energy
2. Bending Moment