Formula for energy stored in a capacitor - Derive

A capacitor can store electric charges and releases them whenever it is required. But how can a capacitor store energy in it? What is the formula of energy stored in a capacitor?

The application of an external voltage across a capacitor produces an electric field between the plates of the capacitor. This electric field moves the charges from one plate to another plate. This introduces a voltage across the capacitor which is different from the voltage of the battery. Electrons continue to move from one plate to another plate until the voltage across the capacitor becomes equal to the voltage of the battery. As the voltage across the capacitor develops, potential energy starts to be stored in the capacitor.

In this article, I’m going to derive and explain the formula of energy stored in a capacitor. This equation for the capacitor energy is very important to study the characteristics of a capacitor.

Contents in this article:

Which type of energy is stored in a capacitor?
Formula for energy stored in a capacitor.

Derivation of energy stored in the capacitor.
How to increase the energy stored in a capacitor?
How to find the energy stored in a capacitor?

Maximum energy stored in a capacitor.
Problems related to energy of a capacitor.

Which type of energy is stored in a capacitor?

The energy stored by a capacitor is the electrostatic potential energy. Such type of energy appears due to the storage of electric charges in the electric field. All types of capacitors like parallel plate capacitors, spherical capacitors, cylindrical capacitors, etc. store the same type of energy inside them.

The unit of energy stored in the capacitor is the same as the unit of energy we know. It is Joule in SI system and erg in CGS system.

Energy stored in capacitor formula

If Q, V and C be the charge, voltage and capacitance of a capacitor, then the formula for energy stored in the capacitor is, $\small {\color{Blue} U=\frac{1}{2}CV^{2}}$ . ……………….(1)

Again, Q = CV. So, we can re-write the equation in two different ways as, $\small {\color{Blue} U=\frac{1}{2}QV}$ …………(2)

And, $\small {\color{Blue} U=\frac{1}{2}\frac{Q^{2}}{C}}$ ……………..(3)

The above three equations give the formula for the energy stored by a capacitor.

Derivation of formula for energy stored in a capacitor

As the charges shifted from one plate to another plate of a capacitor, a voltage develops in the capacitor. This voltage opposes the further shifting of electric charges. Now, to give more charges to the capacitor work is to be done against the voltage drop. This work is stored as the electrostatic potential energy in the capacitor.

Let at any instant the electric charge on the capacitor is q and the voltage is v. Now, to give another dq amount charge to the capacitor, the work done against the developed voltage is, $\small {\color{Blue} dW=v.dq}$

Now, q = C.v or, v = q/C.

Then, $\small {\color{Blue} dW=\frac{q}{C}dq}$

Now, let we want to charge the capacitor up to Q amount from zero value. Then the total work done in charging the capacitor by Q is, $\small {\color{Blue} W=\int_{0}^{Q}\frac{q.dq}{C}}$

or, $\small {\color{Blue} W=\frac{1}{2}CV^{2}}$ …………………..(4)

This work is stored as the electrostatic potential energy (U) of the capacitor and this is the equation for energy stored in a capacitor.

Using Q = CV formula one can re-write this equation in the other two forms.

How to find energy stored in a capacitor?

One can easily determine the energy in a capacitor by using the above formulae. We have to know the values of any two quantities among C, V and Q. One can measure the value of voltage (V) by a voltmeter or multimeter and the capacitance of the capacitor can be determined from the formula for respective capacitors. (See the formula for different types of capacitors).

Again, we can use the energy stored calculator to find the energy of the capacitor.

How to increase the potential energy of a capacitor?

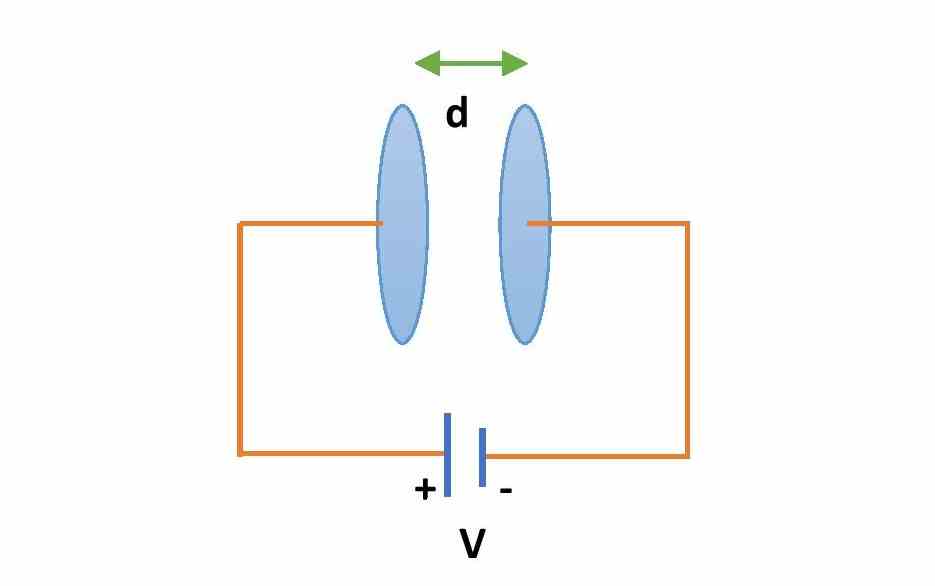
**Parallel plate Capacitor with circular plate**

There are two ways to increase the energy in a capacitor.

By increasing the voltage of the capacitor without changing the parameters and properties of the capacitor.
In the above formulae, one can see that the electrostatic potential energy of the capacitor will increase if the capacitance increases when the voltage remains the same. So, one can increase the energy stored in a parallel plate capacitor by inserting a dielectric medium or slab between the plates at the time of charging the capacitor.

Numerical problems related to the energy of capacitor equation

A parallel plate capacitor is fully charged by 2 coulomb and thereby its potential increases to 3 volts. What will be the maximum energy stored in the parallel plate capacitor?

Answer: Here, the maximum charge of the parallel plate capacitor is 2 C and the corresponding voltage is 3 volts. Then using equation-2 we get,

Energy stored = 1/2 (QV) = (2×3)÷2 = 3 Joule.

2. A parallel plate capacitor has a capacitance of 2 micro-farads. Now, if you place a dielectric medium (K=2) between the plates keeping a battery of 10 voltage on. What will be the ratio of potential energy of the capacitor before and after placing the dielectric medium?

Answer: Here, the battery is always on. So, the voltage is constant at all time. given, V=10 volts, C= 2 micro-farad. After placing the dielectric medium or slab, the capacitance becomes C₂=KC=4 micro-farad.

Now, from equation-1, $\small U=\frac{1}{2}CV^{2}$ .

So, $\small \frac{U_{1}}{U_{2}}=\frac{\frac{CV^{2}}{2}}{\frac{4CV^{2}}{2}}$

or, $\small \frac{U_{1}}{U_{2}}=\frac{1}{4}$

or, U₁ : U₂ = 1 : 4

Thus the final energy in the capacitor increases and becomes four times the initial value of energy.

Some popular questions on this topic:

Where is the energy stored in a capacitor?

Derive the expression for the energy stored in a capacitor.
Deduce the expression for the electrostatic energy stored in a capacitor.
If we insert a dielectric medium in the capacitor keeping the voltage constant, will its potential energy increase or decrease? Explain.

This is all from this article on the formula for the electrostatic energy of a capacitor. If you have any questions on this topic you can ask me in the comment section.

Thank you!

Related posts: