When an electric current flows through a resistor, a voltage drops across it. There is a simple way of measuring the voltage across a resistor by using a voltmeter. But, if we need to calculate it from the circuit parameters, then how can we do that? In this article, I’m going to explain the formula to calculate the voltage drop across a resistor connected in a series or parallel circuit.
Contents in this article:
- Why is there a Voltage drop across a Resistor?
- Formula of voltage drop across a resistor
- Voltage drop across a resistor in series circuit
- Voltage drop across a resistor in Parallel circuit
Why is there a Voltage drop across the Resistors?
A resistor offers opposition to the current flow through it. This opposition is called Resistance. To cross this barrier, electrons need sufficient external energy. An external battery gives such an amount of energy to the electrons. If V is the voltage of an ideal battery (zero internal resistance), then the energy gained by an electron from this battery is eV.
Electrons use this energy to overcome the resistance of a conductor. While passing through the resistor, the electron losses a part of this energy to overcome the resistance of the resistor. That means the electron losses a part of the external voltage that it gained from the battery. In this way, a loss or drop of voltage occurs across a resistor.
Formula for the Voltage drop across a Resistor
Sometimes we need to find the voltage drop across a conductor or resistor to study its conductivity and other properties. If the current and resistance of the resistor are known then potential drop across the resistor can be easily found.
From Ohm’s law we know that if I amount of electric current passes through a resistor of resistance R, then the voltage drop across the resistor will be, V = IR……….(1)
This is the general equation of potential difference across a single resistor. However, the task is not that simple for a circuit containing more than one resistor. Because there are various types of electric circuits and value of electric current will not be the same through every resistor. We have to calculate the resistance and current through it before finding the voltage across the resistance or a combination of resistors. See the following part for that.
Voltage drop across resistors in a series circuit
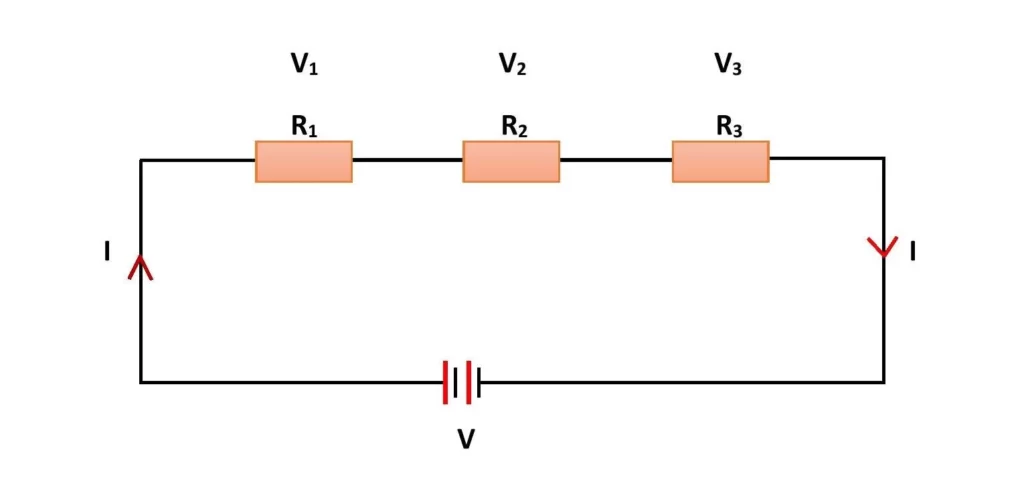
A Series circuit acts like a voltage divider circuit. The supply voltage divides among the resistors in a series circuit. Let three resistors of resistances R1, R2 and R3 respectively are connected in series. There is only one path for the current flow as the resistors are connected in a single line. Hence the amount of electric current through each resistor is the same. If I is the amount of current, then the potential drop across the resistances R1, R2 and R3 are
- V1 = IR1
- V2 = IR2
- V3 = IR3
The amount of voltage drop across individual resistors depends on their resistance value. However, the sum of voltage drops will be equal to the input voltage of the battery. If V is the voltage of the battery, then V = V1+ V2 + V3. If we increase the number of resistors, the current in the circuit decreases and hence the voltage across individual resistors will decrease.
Voltage drop across resistors in Parallel circuit
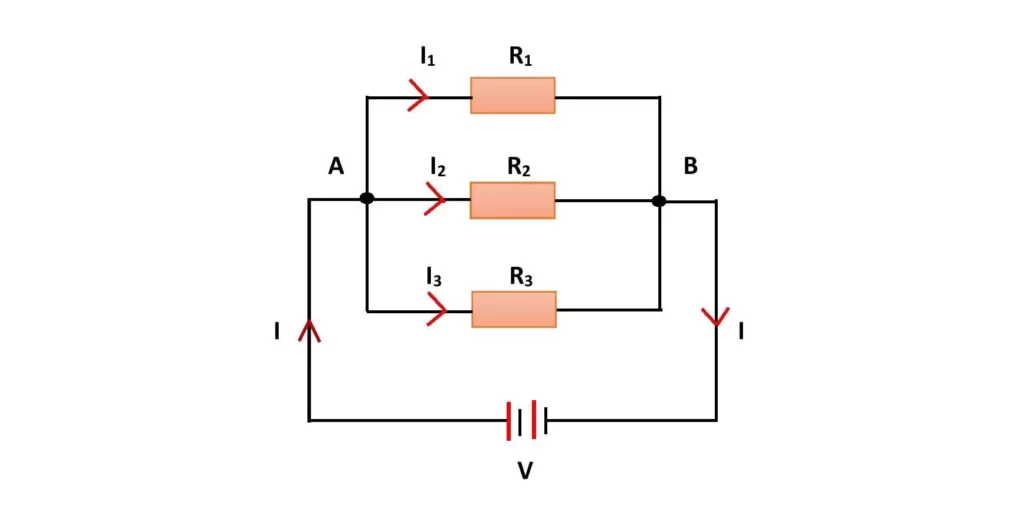
In a parallel circuit, all conductors or resistors are connected across the two same points. The potential difference across each resistor becomes the same which is equal to the voltage of the battery. If we know the voltage of the battery, then the voltages across resistors are easy to find.
If the voltage of the battery source is unknown, then we need to know the current through each resistor. Note that the amount of current is not the same for parallel resistors. If I1, I2 and I3 are the electric currents through the parallel resistors R1, R2 and R3 respectively, then voltages across the resistors are
- across R1 is V1 = I1R1 = V
- across R2 is V2 = I2R2 = V
- across R3 is V3 = I3R3 = V
Where V is the voltage of the battery. Currents through individual resistors can be calculated by using the Shunts rule.
How to calculate voltage drop across resistors in a mixed circuit?
For a mixed circuit, the calculation of electric current through all resistors can be tricky. But those can be calculated through the following steps –
- Find the equivalent resistance (Req) of the mixed circuit.
- Then find the total current from the battery. If V is the voltage of the power supply, then total current, I = V/Req.
- This total current flows through the series resistors and divides among the parallel resistors. Current through the parallel resistors can be found by using Shunt’s rule.
- After finding currents through the resistors, one can easily find the voltage drop across resistors by using the formula of Ohm’s law i.e. V = IR.
This is all from this article on Formula for the voltage drop across a resistor. If you still have any doubts about this topic, you can ask me in the comment section.
Thank you!
Related posts:
- Voltage drop across Capacitor
- Voltage across an Inductor
- Ohm’s Law of current electricity
- Series and Parallel combination of Resistors
- Resistor color code calculation rules
2 thoughts on “Voltage drop across Resistor – formula & concepts”
Comments are closed.