What is Standard Form of a number? See example

by

Here we’re to discuss what is Standard Form in maths and how to write numbers in standard form.

Standard Form, also known as Scientific notation of numbers, is a way to express very large or very small numbers in a more compact and convenient form. It is widely used in maths of scientific and technical fields and everyday life to represent extremely large or small quantities.

In standard form, a number is expressed as a coefficient, or base number, multiplied by a power of 10. For example, the number 7,000,000 can be written in standard form as 7 x 106.
The coefficient, or base number, is 7, and the power of 10, represented by the superscript “6”, indicates that the number should be multiplied by 10 raised to the sixth power, or 1,000,000.

For a number containing multiple non-zero digits, we need to round off the number (up to the required decimal) after expressing it in standard form.

Further in this article, we will study the basic definition of standard form in maths, its advantages, real-life uses, and some mathematical conversions to understand the topic more precisely.

Definition of standard form in Maths

“In mathematics, a standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it provides the simplest representation of an object and allows it to be identified uniquely.”

Advantages of Standard form

The standard form has several advantages over normal forms, especially when dealing with very large or small numbers. It is much easier to read and understand a number written in standard form and takes up less space on a page.

The key advantage of standard form is that it allows us to represent very large or very small numbers using fewer digits, making it easier to read and understand. For example, the approximate distance from the earth to the sun is 93 million miles.

This number can be written in standard form as 9.3 x 107. This is much easier to read and understand than writing out the full number, which would be 93,000,000.

Rules for Standard Form of numbers

We first need to determine the coefficient or base number to express a number in standard form. This is done by moving the decimal point in the original number until it is immediately to the right of the first non-zero digit. For example, consider the number 123,456.

To express this number in standard form, we would move the decimal point six places to the left, resulting in a coefficient of 1.23456.

Next, we need to determine the power of 10 that we will use to multiply the coefficient. This is done by counting the number of places where the decimal point was moved. In the example above, the decimal point was moved six places to the left, so the power of 10 would be 106.

Finally, we multiply the coefficient by the power of 10 to express the number in standard form. In this case, the standard form of 123,456 would be 1.23456 x 106.

Writing a number in Standard Form – Examples

In the above sections, we have discussed the examples theoretically. Now we’ll discuss the step-by-step solution to the problems related to standard form.

Example 1:

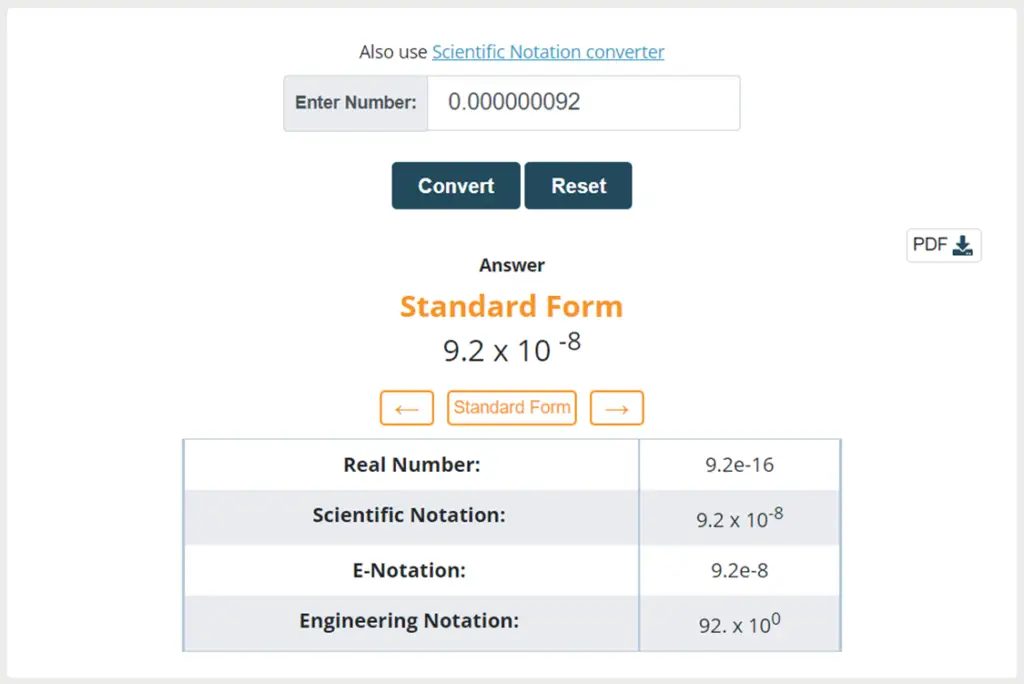
Convert 0.000000092 into standard form

Solution:

Step 1: Write the term

= 0.000000092

Step 2: Determine the position of the decimal  

= 0.000000092

Step 3: Move the decimal to the right side of the 1st non-zero number

= 9.2

Step 4: Count the total number of digits that we have moved and multiply 9.2 with the power of 10, we have moved 8 places so:

= 9.2 x 10-8   

The conversion of smaller and larger numbers into standard form can also be done with the help of a standard form calculator by Meracalculator to ease up calculations.

Example 2:

Convert the number 685000000000 into standard form

Solution:

Step 1: Write the term

= 685000000000

Step 2: Determine the position of the decimal 

= 685000000000.   

Step 3: Move the decimal to the right side of the 1st non-zero number

= 6.85

Step 4: Count the total number of digits that we have moved and multiply 6.85 with the power of 10, we have moved 11 places so:

= 6.85 x 1011  

Real-life uses of Standard Form

Here are a few more examples of numbers expressed in standard form:

  • The distance from the moon to the earth is approximately 238,855 miles. This number can be expressed in standard form as 2.38855 x 105.
  • The mass of a hydrogen atom is approximately 1.67 x 10-27 kilograms.
  • The speed of light in a vacuum is approximately 299,792,458 meters per second. This number can be expressed in standard form as 2.99792458 x 108.

Converting from Standard Form to Normal Form

To convert a number expressed in standard form back to its normal form, we simply need to reverse the process described above. First, we multiply the coefficient by the power of 10. Then, we move the decimal point in the resulting number to its original position.

For example, consider the number 4.7 x 103. To convert this number to its normal form, we would first multiply the coefficient (4.7) by the power of 10 (103). This results in a number of 4700. Next, we would move the decimal point three places to the right, resulting in the normal form of 4700, or 4,700.

Practice problems

1. What is the standard form of 0.00026?

  1. 0.00026
  2. 2.6 x 10-5
  3. 2.6 x 10-6
  4. 2.600000

2. Write 245670000 in standard form

  1. 24567 x 104
  2. 24567 x 10-4
  3. 2.4567 x 108
  4. 2.4567 x 10-8

3. What is the standard form of 0.00000567?

  1. 567 x 105
  2. 567 x 10-5
  3. 5.67 x 107
  4. 5.67 x 10-7

4. Which term is used for writing smaller and larger numbers in an easy way?

  1. Point slope form
  2. Standard form
  3. Slope intercept form
  4. Two points form

5. The product of 2 x 104 and 4 x 103 is:

  1. 8 x 1012
  2. 8 x 107
  3. 12 x 109
  4. 16 x 102

Summary

In this article, we have studied the basic concept of the term “standard form”, its definition, and its key advantages are discussed briefly. The term “standard form” plays a vital role in the field of engineering, the engineers and scientists use it frequently in their daily routines. In the example section, firstly we understand how to write numbers in Standard form and after that, we discussed some real-life uses of this term. Then we discussed mathematical problems to understand the concept of calculating the standard form of a number. Hope this article will help you out in problem-solving.

This is all from this article. If you find this beneficial, please share it with your mates.

Thank You.

Related posts

  1. Significant figures of a number
  2. Rounding off a number